

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a, ta có AB=36cm, E là trung điểm
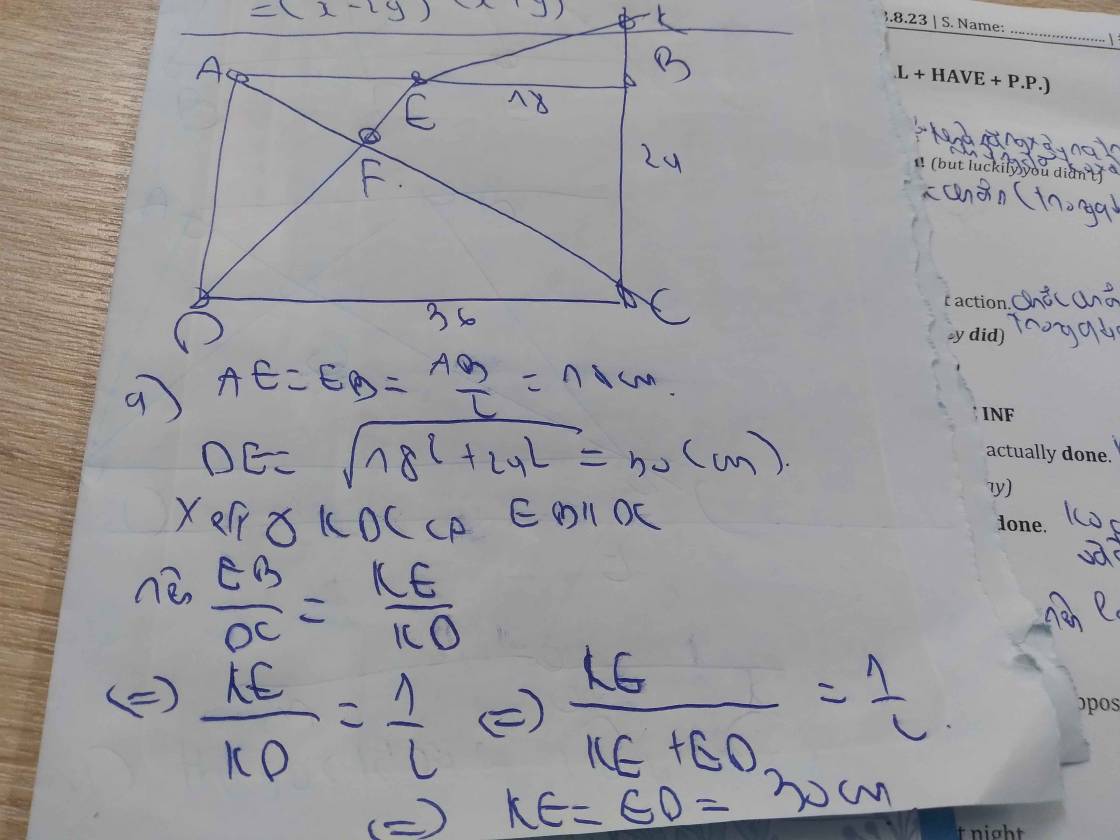
=>AE=EB=\(\frac{36}{2}=18cm\)
Xét tam giác ADE vuông tại A có :
DE2=AD2+AE2(Py-ta-go)
DE2=242+182
=>DE=30cm
ta có ABCD là hcn => AD//BC(t/c)
mà G \(\in\)BC
=>GC//AD
Xét tam giác ADE và tam giác BGE có :
\(\widehat{EAD}\)=\(\widehat{GBE}\)=900
\(\widehat{ADE}\)=\(\widehat{BGE}\)(So le trong vì GC//AD)
=>\(\Delta ADE=\Delta BGE\)(Cạnh góc vuông-góc nhọn kề cạnh)
=>DE=GE(2 cạnh t/ứ)
mà DE=30cm(cmt)
=>GE=30cm
Lại có E \(\in\)DG
=>DE+GE=DG
Thay số: 30+30=60
=>DG=60cm.

a: AE=EB=AB/2=18cm
\(DE=\sqrt{24^2+18^2}=30\left(cm\right)\)
\(AC=\sqrt{36^2+24^2}=12\sqrt{13}\left(cm\right)\)
\(DF=\dfrac{DA\cdot DC}{AC}=\dfrac{36\cdot24}{12\sqrt{13}}=\dfrac{72\sqrt{13}}{13}\left(cm\right)\)
b: Xét ΔFAE vuông tại F và ΔFGC vuông tại F có
\(\widehat{FAE}=\widehat{FGC}\)
Do đo: ΔFAE\(\sim\)ΔFGC
Suy ra: FA/FG=FE/FC
=>\(FE\cdot FG=FA\cdot FC=FD^2\)

A B C D E F G
Cô hướng dẫn nhé :)
a. \(\Delta AEF\sim\Delta CDF\left(g-g\right)\)
b. Ta thấy AB song song DC nên áp dụng Talet ta có:
\(\frac{EF}{FD}=\frac{AE}{DC}=\frac{1}{2}\)
Lại có: \(\Delta AED=\Delta BEG\left(g-c-g\right)\) nên ED = EG.
Ta thấy \(\frac{FD}{FG}=\frac{2EF}{EF+3EF}=\frac{1}{2}\)
\(\Rightarrow\frac{EF}{FD}=\frac{FD}{FG}\Rightarrow FD^2=EF.FG\)
C. Tính DE ta chỉ cần dùng định lý Pitago là xong rồi :)
Chúc em học tốt :))

a) \(E\) là trung điểm \(AB\) nên \(AE=EB=\dfrac{AB}{2}=18\left(cm\right)\)
Áp dụng định lí Pi-ta-go ta có:
\(DE^2=AD^2+AE^2\)
\(\Leftrightarrow DE^2=24^2+18^2\)
\(\Leftrightarrow DE=30\left(cm\right)\)
Áp dụng định lí Ta-let ta có:
\(AD\text{/ / }BC\Rightarrow AD\text{/ / }BG\Rightarrow\dfrac{DE}{EG}=\dfrac{AD}{BG}=\dfrac{AE}{EB}=1\)
\(\Rightarrow DE=EG=30\left(cm\right)\Rightarrow DG=60\left(cm\right)\)
\(AE\text{/ / }DC\Rightarrow\dfrac{AF}{FC}=\dfrac{EF}{DF}=\dfrac{AF}{DC}=\dfrac{1}{2}\)
\(\Rightarrow EF=\dfrac{1}{2}DF\Rightarrow EF=\dfrac{1}{3}DE=10\left(cm\right)\)
\(\Rightarrow DE=DE-EF=20\left(cm\right)\)
b)
Ta có :
\(FD^2=\left(\dfrac{2}{3}DE\right)^2=\dfrac{4}{9}DE^2\)
\(\Rightarrow FD^2=FE.FG\)