Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn ơi K thuộc SD hả ? ... nếu vậy thì MK sẽ không thể song song với mặt phẳng ( SBC) đâu nhé :)

Ta có: OF là đường trung bình tam giác SAC
\(\Rightarrow OF//SA\Rightarrow OF//\left(SAD\right)\)
OE là đường trung bình tam giác SBD
\(\Rightarrow OE//SD\Rightarrow OE//\left(SAD\right)\)
\(\Rightarrow\left(OEF\right)//\left(SAD\right)\)

a.
Do M là trung điểm SA, O là trung điểm AC
\(\Rightarrow OM\) là đường trung bình tam giác SAC \(\Rightarrow OM||SC\Rightarrow OM||\left(SBC\right)\) (1)
N là trung điểm CD, O là trung điểm AC \(\Rightarrow ON\) là đường trung bình ACD
\(\Rightarrow ON||AD\Rightarrow ON||BC\Rightarrow ON||\left(SBC\right)\) (2)
Mà \(ON\cap OM=O\) ; \(OM;ON\in\left(OMN\right)\) (3)
(1);(2);(3) \(\Rightarrow\left(OMN\right)||\left(SBC\right)\)
b.
J cách đều AB, CD \(\Rightarrow J\) thuộc đường thẳng d qua O và song song AB, CD
- Nếu J trùng O \(\Rightarrow OI\) là đường trung bình tam giác SBD \(\Rightarrow OI||SB\Rightarrow OI||\left(SAB\right)\)
Hay \(IJ||\left(SAB\right)\)
- Nếu J không trùng O, ta có \(\left\{{}\begin{matrix}IO||SB\left(đtb\right)\Rightarrow IO||\left(SAB\right)\\d||AB\Rightarrow IJ||AB\Rightarrow OJ||\left(SAB\right)\end{matrix}\right.\)
\(\Rightarrow\left(OIJ\right)||\left(SAB\right)\Rightarrow IJ||\left(SAB\right)\)
a.
Do M là trung điểm SA, O là trung điểm AC
⇒��⇒OM là đường trung bình tam giác SAC ⇒��∣∣��⇒��∣∣(���)⇒OM∣∣SC⇒OM∣∣(SBC) (1)
N là trung điểm CD, O là trung điểm AC ⇒��⇒ON là đường trung bình ACD
⇒��∣∣��⇒��∣∣��⇒��∣∣(���)⇒ON∣∣AD⇒ON∣∣BC⇒ON∣∣(SBC) (2)
Mà ��∩��=�ON∩OM=O ; ��;��∈(���)OM;ON∈(OMN) (3)
(1);(2);(3) ⇒(���)∣∣(���)⇒(OMN)∣∣(SBC)
b.
J cách đều AB, CD ⇒�⇒J thuộc đường thẳng d qua O và song song AB, CD
- Nếu J trùng O ⇒��⇒OI là đường trung bình tam giác SBD ⇒��∣∣��⇒��∣∣(���)⇒OI∣∣SB⇒OI∣∣(SAB)
Hay ��∣∣(���)IJ∣∣(SAB)
- Nếu J không trùng O, ta có {��∣∣��(đ��)⇒��∣∣(���)�∣∣��⇒��∣∣��⇒��∣∣(���){IO∣∣SB(đtb)⇒IO∣∣(SAB)d∣∣AB⇒IJ∣∣AB⇒OJ∣∣(SAB)
⇒(���)∣∣(���)⇒��∣∣(���)⇒(OIJ)∣∣(SAB)⇒IJ∣∣(SAB)

a.
Do O là tâm hbh \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow OJ\) là đường trung bình tam giác SAC
\(\Rightarrow OJ||SA\)
Mà \(SA\in\left(SAC\right)\Rightarrow OJ||\left(SAC\right)\)
\(SA\in\left(SAB\right)\Rightarrow OJ||\left(SAB\right)\)
b. O là trung điểm BD, I là trung điểm BC
\(\Rightarrow OI\) là đườngt rung bình tam giác BCD
\(\Rightarrow OI||CD\)
Mà \(CD\in\left(SCD\right)\Rightarrow OI||\left(SCD\right)\)
Tương tự ta có IJ là đường trung bình tam giác SBC \(\Rightarrow IJ||SB\Rightarrow IJ||\left(SBD\right)\)
c. Ta có I là trung điểm BC, O là trung điểm AC
\(\Rightarrow M\) là trọng tâm tam giác ABC
\(\Rightarrow BM=\dfrac{2}{3}BO=\dfrac{2}{3}.\dfrac{1}{2}BD=\dfrac{1}{3}BD\)
\(\Rightarrow\dfrac{BM}{BD}=\dfrac{1}{3}\)
Theo giả thiết \(SK=\dfrac{1}{2}KD=\dfrac{1}{2}\left(SD-SK\right)\Rightarrow SK=\dfrac{1}{3}SD\)
\(\Rightarrow\dfrac{SK}{SD}=\dfrac{1}{3}=\dfrac{BM}{BD}\Rightarrow KM||SB\) (Talet đảo)
\(\Rightarrow MK||\left(SBC\right)\)


Đáp án A
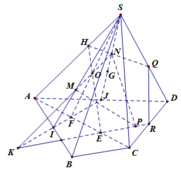
Tam giác SAB có I là trọng tâm và E là trung điểm của AB
Nên ta có S I S E = 2 3 (1)
Tam giác SAD có J là trọng tâm và F là trung điểm của AD
Nên ta có S J S F = 2 3 (2)
Từ (1) và (2) ta có: IJ // EF (3) (định lý Ta-lét trong tam giác SEF)
Tam giác ABD có EF là đường trung bình nên EF // BD (4)
Từ (3) và (4) suy ra IJ // BD
Mà BD (SBD)
Do đó IJ // (SBD).