Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
a.
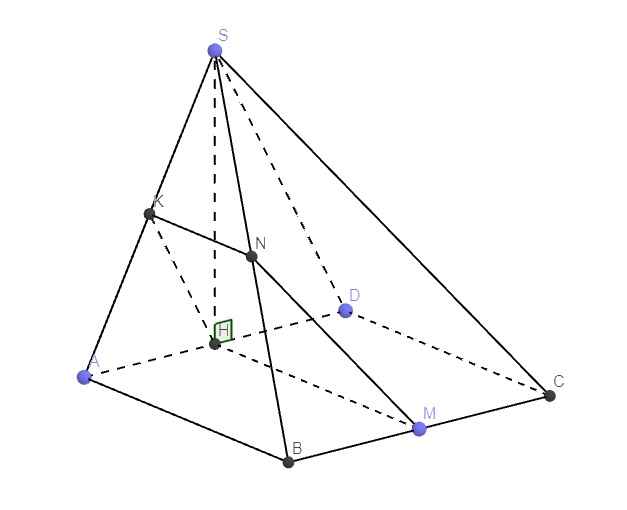
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(\Rightarrow CD\perp SD\Rightarrow\Delta SCD\) vuông tại D
b.
Do H là trung điểm AD, K là trung điểm SA
\(\Rightarrow KH\) là đường trung bình tam giác SAD
\(\Rightarrow KH||SD\Rightarrow KH||\left(SCD\right)\)
H là trung điểm AD, M là trung điểm BC \(\Rightarrow HM||CD\)
\(\Rightarrow HM||\left(SCD\right)\)
Mà HM cắt KH tại H
\(\Rightarrow\left(HKM\right)||\left(SCD\right)\)
c.
Qua K kẻ đường thẳng song song AB cắt SB tại N
\(\Rightarrow N=\left(HKM\right)\cap SB\)
\(\left\{{}\begin{matrix}KN||AB\\HM||AB\end{matrix}\right.\) \(\Rightarrow KN||HM\) (1)
Mặt khác \(\left\{{}\begin{matrix}HM||CD\\CD||\left(SAD\right)\end{matrix}\right.\) \(\Rightarrow HM\perp\left(SAD\right)\Rightarrow HM\perp KH\) (2)
(1);(2) \(\Rightarrow\) HKNM là hình thang vuông

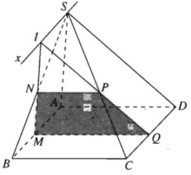
a) Vì M ∈ (SAB)
Và 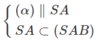 nên (α) ∩ (SAB) = MN
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và 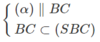 nên (α) ∩ (SBC) = NP
nên (α) ∩ (SBC) = NP
và NP // BC (1)
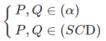 ⇒ (α) ∩ (SCD) = PQ
⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và 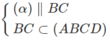 nên (α) ∩ (ABCD) = QM
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
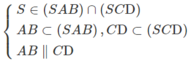 ⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒ 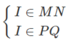
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.

Chà, bài này dựng xong hình là xong thôi (tính toán đơn giản bằng Talet)
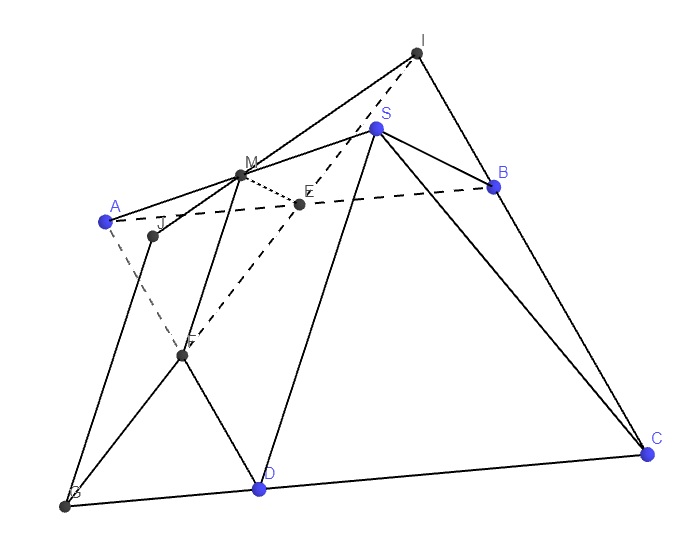
Đầu tiên là dựng mp qua M và song song (SBD): qua M kẻ các đường thẳng song song SB, SD lần lượt cắt AB, AD tại E và F
Nối EF kéo dài cắt BC tại I và CD tại G
Qua G kẻ đường thẳng song song MF (hoặc SD) cắt MI kéo dài tại J
Talet cho ta: \(\dfrac{MI}{MJ}=\dfrac{IF}{GF}\)
Mà \(\dfrac{GF}{GI}=\dfrac{DF}{BI}=\dfrac{\dfrac{1}{2}AD}{BC+\dfrac{1}{2}BC}=...\)
Vậy là xong

Đáp án D
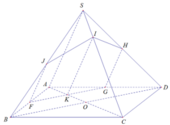
Trong (ABCD), kẻ đường thẳng d đi qua F và song song với BD
d cắt AD tại G
d cắt AC tại K ⇒ F G ∩ A C = K
Trong (SAD), kẻ đường thẳng x đi qua G và song song với SA
x cắt SD tại H
Trong (SAB), kẻ đường thẳng y đi qua F và song song với SA
y cắt SB tại J
Trong (SAC), kẻ đường thẳng z đi qua K và song song với SA
z cắt AC tại I
⇒ FGHIK là thiết diện cần tìm
⇒ thiết diện là ngũ giác