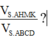Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(SM=MA=SA-SM\Rightarrow SM=\dfrac{1}{2}SA\)
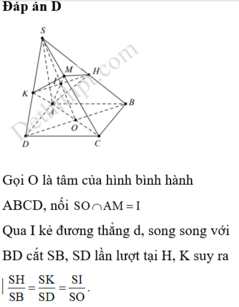
Do IM song song SO, áp dụng định lý Talet trong tam giác SAO:
\(\dfrac{IO}{OA}=\dfrac{SM}{SA}=\dfrac{1}{2}\)
Do NK song song SO, áp dụng định lý Talet cho tam giác SCO:
\(\dfrac{OK}{OC}=\dfrac{SN}{SC}=\dfrac{1}{3}\)
Mà ABCD là hình bình hành nên \(OA=OC\)
\(\Rightarrow\dfrac{OI}{OK}=\dfrac{3}{2}\)

Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)

Chà, bài này dựng xong hình là xong thôi (tính toán đơn giản bằng Talet)
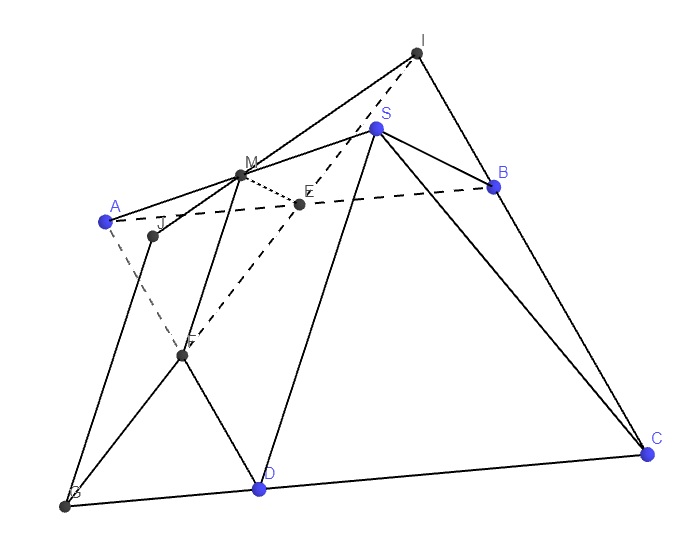
Đầu tiên là dựng mp qua M và song song (SBD): qua M kẻ các đường thẳng song song SB, SD lần lượt cắt AB, AD tại E và F
Nối EF kéo dài cắt BC tại I và CD tại G
Qua G kẻ đường thẳng song song MF (hoặc SD) cắt MI kéo dài tại J
Talet cho ta: \(\dfrac{MI}{MJ}=\dfrac{IF}{GF}\)
Mà \(\dfrac{GF}{GI}=\dfrac{DF}{BI}=\dfrac{\dfrac{1}{2}AD}{BC+\dfrac{1}{2}BC}=...\)
Vậy là xong