Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD.\)
\(ABCD\) là hình vuông \(\Rightarrow CD\perp AD.\)
\(\Rightarrow CD\perp\left(SAD\right).\)
\(\Rightarrow A\)


a) Ta có:
\(\left. \begin{array}{l}M \in SA \subset \left( {SAC} \right)\\N \in SC \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow MN \subset \left( {SAC} \right)\)
b) Ta có:
\(\left. \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\)

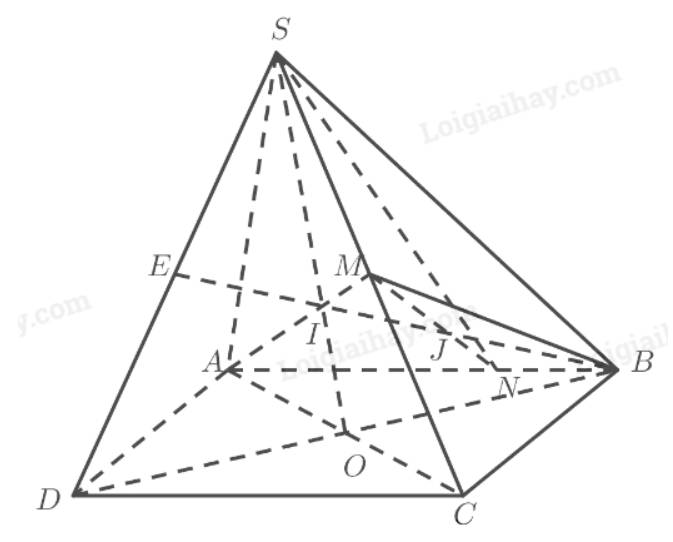
a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(I\) là giao điểm của \(AM\) và \(SO\). Ta có:
\(\left. \begin{array}{l}I \in SO \subset \left( {SB{\rm{D}}} \right)\\I \in AM\end{array} \right\} \Rightarrow I = AM \cap \left( {SB{\rm{D}}} \right)\)
Xét tam giác \(SAC\) có:
\(ABCD\) là hình bình hành \( \Rightarrow O\) là trung điểm của \(AC\)
Theo đề bài ta có \(M\) là trung điểm của \(SC\)
Mà \(I = SO \cap AM\)
\( \Rightarrow I\) là trọng tâm của .
b) Gọi \(E\) là giao điểm của \(S{\rm{D}}\) và \(BI\). Ta có:
\(\left. \begin{array}{l}E \in BI \subset \left( {ABM} \right)\\E \in S{\rm{D}}\end{array} \right\} \Rightarrow E = S{\rm{D}} \cap \left( {ABM} \right)\)
c) Gọi \(J\) là giao điểm của \(MN\) và \(BE\). Ta có:
\(\left. \begin{array}{l}J \in BE \subset \left( {SB{\rm{D}}} \right)\\J \in MN\end{array} \right\} \Rightarrow J = MN \cap \left( {SB{\rm{D}}} \right)\)

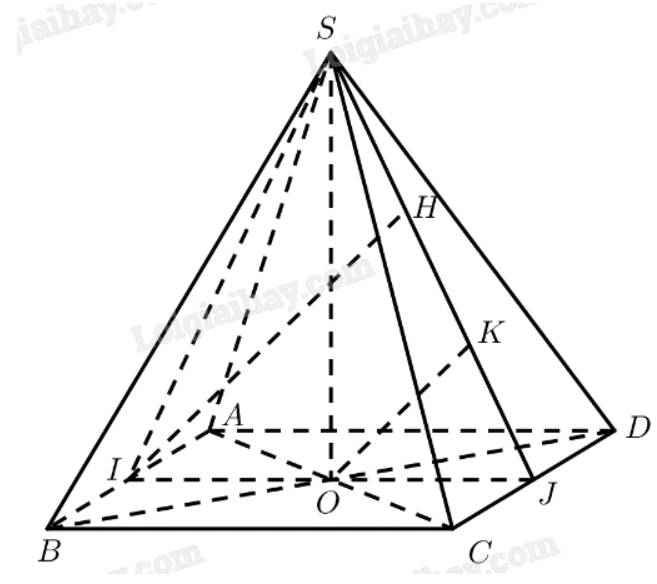
a) Gọi \(O\) là tâm của đáy
\( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AB\)
\(I\) là trung điểm của \(AB\)
\(J\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow IJ\) là đường trung bình của hình vuông \(ABCD\)
\(\left. \begin{array}{l} \Rightarrow IJ\parallel A{\rm{D}}\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow IJ \bot AB\)
Ta có:
\(\left. \begin{array}{l}SO \bot AB\\IJ \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {SIJ} \right)\)
b) Kẻ \(IH \bot SJ\left( {H \in SJ} \right),OK \bot SJ\left( {K \in SJ} \right) \Rightarrow IH\parallel OK\)
\(O\) là trung điểm của \(IJ \Rightarrow IH = 2{\rm{O}}K\)
Ta có:
\(\left. \begin{array}{l}AB\parallel C{\rm{D}}\\C{\rm{D}} \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {AB,SC} \right) = d\left( {AB,\left( {SC{\rm{D}}} \right)} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}\left. \begin{array}{l}AB \bot \left( {SIJ} \right)\\C{\rm{D}}\parallel AB\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SIJ} \right) \Rightarrow C{\rm{D}} \bot IH\\ & IH \bot SJ\end{array} \right\} \Rightarrow IH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {AB,C{\rm{D}}} \right) = d\left( {AB,\left( {SC{\rm{D}}} \right)} \right) = IH\end{array}\)
\(O\) là trung điểm của \(IJ\), \(IH\parallel {\rm{O}}K\)\( \Rightarrow IH = 2{\rm{O}}K\)
\(O\) là trung điểm của \(B{\rm{D}}\)
\(J\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow OJ\) là đường trung bình của \(\Delta BCD\)
\( \Rightarrow OJ = \frac{1}{2}BC = \frac{a}{2}\)
\(\Delta ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SAO\) vuông tại \(O\)\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \frac{{a\sqrt 6 }}{2}\)
\(\Delta SOJ\) vuông tại \(O\) có đường cao \(OK\)
\( \Rightarrow OK = \frac{{SO.OJ}}{{\sqrt {S{O^2} + O{J^2}} }} = \frac{{a\sqrt {42} }}{{14}}\)
\( \Rightarrow d\left( {AB,C{\rm{D}}} \right) = IH = 2OK = \frac{{a\sqrt {42} }}{7}\)

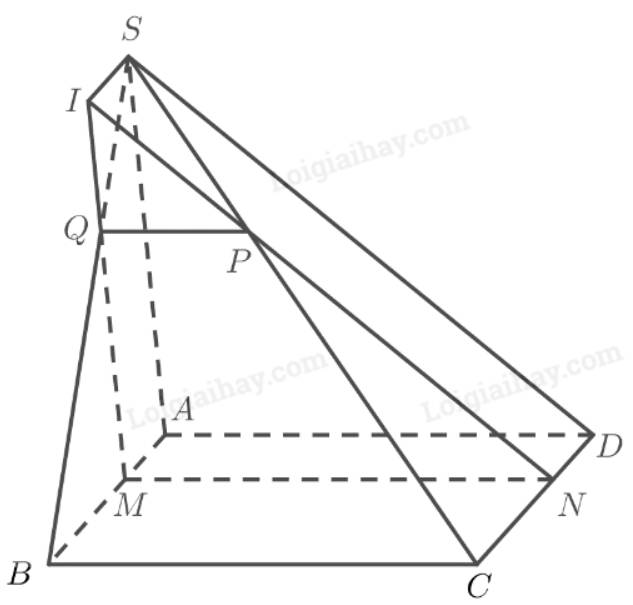
a) Ta có:
\(\left. \begin{array}{l}\left( \alpha \right) \cap \left( {SBC} \right) = PQ\\\left( \alpha \right) \cap \left( {ABCD} \right) = MN\\\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\end{array} \right\} \Rightarrow MN\parallel PQ\parallel BC\)
\( \Rightarrow MNPQ\) là hình thang (1).
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {SAB} \right) = MQ\\\left( {SA{\rm{D}}} \right) \cap \left( {SAB} \right) = SA\end{array} \right\} \Rightarrow MQ\parallel SA \Rightarrow \frac{{MQ}}{{SA}} = \frac{{BM}}{{AB}}\)
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {SC{\rm{D}}} \right) = NP\\\left( {SA{\rm{D}}} \right) \cap \left( {SC{\rm{D}}} \right) = SD\end{array} \right\} \Rightarrow NP\parallel SD \Rightarrow \frac{{NP}}{{SD}} = \frac{{CN}}{{C{\rm{D}}}}\)
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right) = MN\\\left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = AD\end{array} \right\} \Rightarrow MN\parallel AD\parallel BC \Rightarrow \frac{{BM}}{{AB}} = \frac{{CN}}{{C{\rm{D}}}}\)
\( \Rightarrow \frac{{MQ}}{{SA}} = \frac{{NP}}{{S{\rm{D}}}}\)
Mà tam giác \(SAD\) đều nên \(SA = S{\rm{D}}\)
\( \Rightarrow MQ = NP\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow MNPQ\) là hình thang cân.
b) Gọi \(I = MQ \cap NP\). Ta có:
\(\left. \begin{array}{l}\left( {SAB} \right) \cap \left( {SA{\rm{D}}} \right) = SI\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SC{\rm{D}}} \right) \cap \left( {ABCD} \right) = C{\rm{D}}\end{array} \right\} \Rightarrow SI\parallel AB\parallel C{\rm{D}}\)
\(SI\parallel N{\rm{D}},S{\rm{D}}\parallel NI \Rightarrow SIN{\rm{D}}\) là hình bình hành \( \Rightarrow S{\rm{D}} = NI\)
\(SI\parallel MA,S{\rm{A}}\parallel MI \Rightarrow SIMA\) là hình bình hành \( \Rightarrow S{\rm{A}} = MI\)
Xét tam giác \(IMN\) và tam giác \(SAD\) có: \(MN\parallel A{\rm{D,}}MI\parallel SA,NI\parallel S{\rm{D}},MN = A{\rm{D}}\)
tam giác \(IMN\) là tam giác đều cạnh \(a\).
\(\begin{array}{l}SI\parallel AB \Rightarrow \frac{{SI}}{{BM}} = \frac{{IQ}}{{QM}} \Leftrightarrow \frac{{SI}}{{BM + SI}} = \frac{{IQ}}{{QM + IQ}} \Leftrightarrow \frac{{SI}}{{BM + MA}} = \frac{{IQ}}{{QM + IQ}}\\ \Leftrightarrow \frac{{SI}}{{AB}} = \frac{{IQ}}{{MI}} \Leftrightarrow IQ = \frac{{SI.MI}}{{AB}} = \frac{{x.a}}{a} = x\end{array}\)
\({S_{IMN}} = \frac{{{a^2}\sqrt 3 }}{4},{S_{IPQ}} = \frac{{{x^2}\sqrt 3 }}{4} \Rightarrow {S_{MNPQ}} = {S_{IMN}} - {S_{IPQ}} = \frac{{{a^2}\sqrt 3 }}{4} - \frac{{{x^2}\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{4}\left( {{a^2} - {x^2}} \right)\)

Tham khảo hình vẽ:
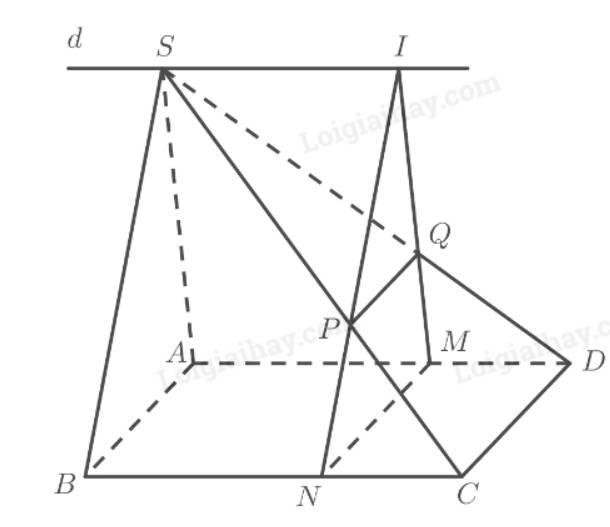
a) Ta có:
\(\begin{array}{l}MN = \left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {SC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\PQ = \left( \alpha \right) \cap \left( {SC{\rm{D}}} \right)\\MN\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel C{\rm{D}}\parallel PQ\).
\( \Rightarrow MNPQ\) là hình bình hành.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in MQ \Rightarrow I \in \left( {SA{\rm{D}}} \right)\\I \in NP \Rightarrow I \in \left( {SBC} \right)\end{array} \right\} \Rightarrow I \in \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\ \Rightarrow SI = \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC\parallel A{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(A{\rm{D}}\parallel BC\parallel SI\).
Vậy \(I\) luôn luôn thuộc đường thẳng \(d\) đi qua \(S\) song song với \(AD\) và \(BC\) cố định khi \(M\) di động trên \(AD\).

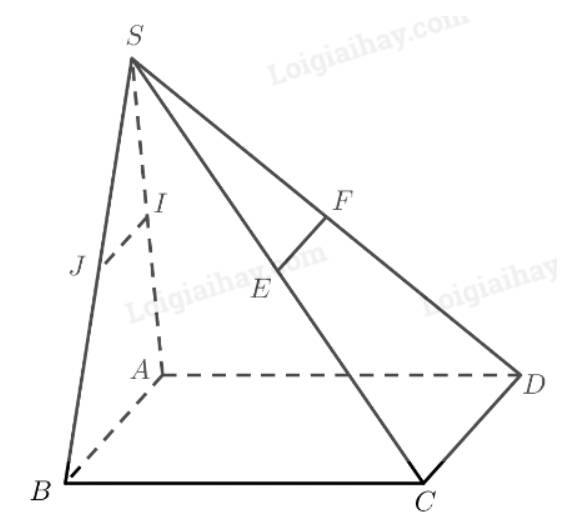
Ta có: \(I\) là trung điểm của \(SA\)
\(J\) là trung điểm của \(SB\)
\( \Rightarrow IJ\) là đường trung bình của tam giác \(SAB\)
\( \Rightarrow IJ\parallel AB\)
\(E\) là trung điểm của \(SC\)
\(F\) là trung điểm của \(SD\)
\( \Rightarrow EF\) là đường trung bình của tam giác \(SC{\rm{D}}\)
\( \Rightarrow EF\parallel C{\rm{D}}\)
Mà \(AB\parallel C{\rm{D}}\).
Vậy \(IJ\parallel EF\parallel AB\parallel C{\rm{D}}\).
Vậy \(AD\) không song song với \(IJ\)
Chọn C.

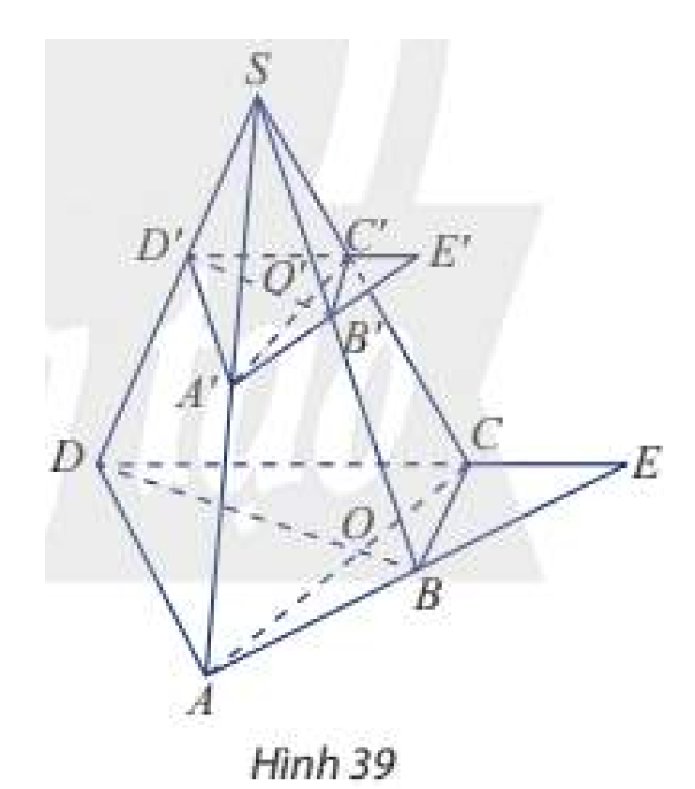
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in BD \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}O' \in A'C' \subset \left( {SAC} \right)\\O' \in B'D' \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O' \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\)
Do đó, \(S,O,O'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).
Vậy \(S,O',O\) thẳng hàng.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}E \in AB \subset \left( {SAB} \right)\\E \in CD \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\\\left. \begin{array}{l}E' \in A'B' \subset \left( {SAB} \right)\\E' \in C'D' \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E' \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\)
Do đó, \(S,E,E'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SC{\rm{D}}} \right)\).
Vậy \(S,E,E'\) thẳng hàng.
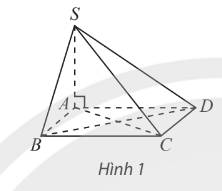


Ta có:
\(\begin{array}{l}\left. \begin{array}{l}S \in \left( {SAC} \right)\\S \in \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow S \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}M \in AC \subset \left( {SAC} \right)\\M \in B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow M \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\) là đường thẳng \(SM\).
Chọn A.