

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



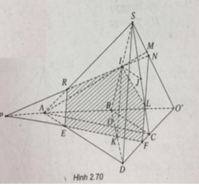
a) Gọi O′ = AB ∩ CD, M = AI ∩ SO′
Ta có: M = AI ∩ (SCD)
b) IJ // BC ⇒ IJ // AD ⇒ IJ // (SAD)
c) Đường thẳng qua I song song với SD cắt BD tại K.
Do 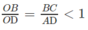 nên OB < OD. Do đó điểm K thuộc đoạn OD.
nên OB < OD. Do đó điểm K thuộc đoạn OD.
Qua K, kẻ đường thẳng song song với AC cắt DA, DC, BA lần lượt tại E, F, P.
Gọi R = IP ∩ SA. Kéo dài PI cắt SO’ tại N
Gọi L = NF ∩ SC
Ta có thiết diện là ngũ giác IREFL.

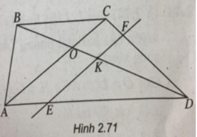
Kéo dài AB và CD cắt nhau tại E
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
Qua M kẻ đường thẳng d song song CD lần lượt cắt AC và AD tại F và G
Trong mp (SAC), qua F kẻ đường thẳng song song SA cắt SC tại P
Trong mp (SAD), qua G kẻ đường thẳng song song SA cắt SD tại Q
\(\Rightarrow\) Hình thang MPQG là thiết diện của (P) và chóp

a) Ta có:
- M là trung điểm của AB, nên M là trung điểm của đoạn thẳng AB.
- P là trung điểm của SC, nên P là trung điểm của đoạn thẳng SC.
- I là trung điểm của SB, nên I là trung điểm của đoạn thẳng SB.
Vì M, P, I lần lượt là trung điểm của các đoạn thẳng AB, SC, SB, nên ta có:
2AM = AB, 2CP = CS, 2BI = BS.
Giả sử BC không song song với MP. Khi đó, ta có:
- MP cắt BC tại H.
- MP cắt SA tại K.
- MP cắt QN tại L.
Theo định lý , ta có:
AH/HC = AK/KS = AL/LQ.
Từ đó, ta có:
2AM/2CP = AK/KS = AL/LQ.
Tuy nhiên, ta đã biết rằng 2AM/2CP = AB/CS = BS/CS = BI/CS = 2BI/2CP.
Vậy ta có:
2BI/2CP = AK/KS = AL/LQ.
Do đó, ta có AK = AL và KS = LQ.
Từ đó, ta suy ra K = L và Sẽ có MP song song với BC.
Vậy BC // (IMP).
b) Thiết diện của mặt phẳng (α) với hình chóp là một hình tam giác. Để xác định hình tam giác này, cần biết thêm thông tin về góc giữa mặt phẳng (α) và mặt phẳng đáy ABC.
c) Đường thẳng CN và mặt phẳng (SMQ) giao nhau tại một điểm. Để tìm giao điểm này, cần biết thêm thông tin về góc giữa đường thẳng CN và mặt phẳng (SMQ).
--thodagbun--
(Bn tham khảo cách lm đy nhe )

a: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
b: Xét ΔSAB có
M,N lần lượt là trung điểm của AS,AB
=>MN là đường trung bình của ΔSAB
=>MN//SB
Ta có: MN//SB
SB\(\subset\)(SBC)
MN ko nằm trong mp(SBC)
Do đó: MN//(SBC)

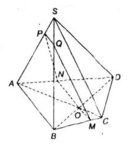
+ Ta có: (α) // AB
⇒ giao tuyến (α) và (ABCD) là đường thẳng qua O và song song với AB.
Qua O kẻ MN // AB (M ∈ BC, N ∈ AD)
⇒ (α) ∩ (ABCD) = MN.
+ (α) // SC
⇒ giao tuyến của (α) và (SBC) là đường thẳng qua M và song song với SC.
Kẻ MQ // SC (Q ∈ SB).
+ (α) // AB
⇒ giao tuyến của (α) và (SAB) là đường thẳng qua Q và song song với AB.
Từ Q kẻ QP // AB (P ∈ SA).
⇒ (α) ∩ (SAD) = PN.
Vậy thiết diện của hình chóp cắt bởi (α) là tứ giác MNPQ.
Ta có: PQ// AB và NM // AB
=> PQ // NM
Do đó, tứ giác MNPQ là hình thang.