Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

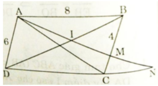
a) AD // BC (gt)![]()
b) Xét ΔAMB và ΔNAD có:
∠BAM = ∠ AND (so le trong, AB // CD)
∠ABM = ∠ADN (góc đối của hình bình hành)
⇒ ΔAMB ∼ ΔNAD (g.g)
c) ΔAMB ∼ ΔNAD (cmt)
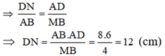
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)
d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
![]()
Tương tự, do AD // BM nên
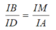
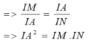

A B C D M I N 8 cm 6 cm 1 1 1 2 2 1 2 3 4
a) Ta có: ABCD là hình bình hành (1)
\(\Rightarrow AD\) // BC
\(\Rightarrow\widehat{M_1}=\widehat{A_1}\) (2 góc so le trong) (2)
Xét \(\Delta IMB\) và \(\Delta IAD\) ta có:
\(\widehat{I_1}=\widehat{I_2}\) (2 góc đối đỉnh) (3)
Từ (2), (3) \(\Rightarrow\Delta IMB\sim\Delta IAD\) (G-G) (4)
Từ (4) \(\Rightarrow\dfrac{IB}{ID}=\dfrac{MB}{AD}=\dfrac{4}{6}=\dfrac{2}{3}\)
b) Từ (1) \(\Rightarrow AB\) // CD \(\Rightarrow\) AB // ND
\(\Rightarrow\widehat{A_2}=\widehat{N_1}\) (5)
Từ (1) \(\Rightarrow\widehat{ABC}=\widehat{CDA}\) (2 góc đối của hình bình hành) (6)
Từ (5), (6) \(\Rightarrow\Delta AMB\sim\Delta AND\) (G-G)
c) Từ (1) \(\Rightarrow AD=BC=6\left(cm\right)\)
Ta có: \(MC=BC-MB=6-4=2\left(cm\right)\)
Xét \(\Delta MNC\) và \(\Delta MAB\) ta có:
\(\widehat{M_1}=\widehat{M_2}\) (2 góc đối đỉnh) (7)
Từ (5), (7) \(\Rightarrow\Delta MNC\sim\Delta MAB\) (G-G) (8)
Từ (8) \(\Rightarrow\dfrac{MC}{MB}=\dfrac{NC}{AB}\Leftrightarrow\dfrac{2}{4}=\dfrac{NC}{8}\)
\(\Leftrightarrow NC=\dfrac{2.8}{4}=4\left(cm\right)\)
Từ (1) \(\Rightarrow AB=CD=8\left(cm\right)\)
\(\Rightarrow\) DN = CD + NC = 8 + 4 = 12 (cm)
d) Xét \(\Delta IAB\) và \(\Delta IND\) ta có:
\(\widehat{I_3}=\widehat{I_4}\) (2 góc đối đỉnh) (9)
Từ (5), (9) \(\Rightarrow\Delta IAB\sim\Delta IND\) (G-G) (10)
Từ (10) \(\Rightarrow\dfrac{IA}{IN}=\dfrac{IB}{ID}\) (11)
Từ (4) \(\Rightarrow\dfrac{IM}{IA}=\dfrac{IB}{ID}\) (12)
Từ (11), (12) \(\Rightarrow\dfrac{IA}{IN}=\dfrac{IM}{IA}\Leftrightarrow IA^2=IN.IM\)
Nếu hình vẽ không rõ thì có thể vào góc học tập của mình xem

Từ (1) ⇒AB⇒AB // CD ⇒⇒ AB // ND
⇒ˆA2=ˆN1⇒A2^=N1^ (5)
Từ (1) ⇒ˆABC=ˆCDA⇒ABC^=CDA^ (2 góc đối của hình bình hành) (6)
Từ (5), (6) ⇒ΔAMB∼ΔAND⇒ΔAMB∼ΔAND (G-G)

a. Tứ giác ABCD là hình bình hành.
\(\Rightarrow AB=CD\)(tính chất hình bình hành)
và \(AB//CD\Rightarrow\widehat{ABD}=\widehat{BDC}\)(so le trong)
Xét \(\Delta AMB\)và \(\Delta CND\)có:
\(AB=CD\)(cmt)
\(\widehat{ABM}=\widehat{CDN}\)(cmt)
\(BM=DN\)(GT)
\(\Rightarrow\Delta AMB=\Delta CND\left(c.g.c\right)\)
b. Có AC cắt BD tại O
=> O là trung điểm của AC => OA = OC.
=> O là trung điểm của BD => OB = OD.
Có OB = OM + MD
OD = ON + ND
mà OB = OD, MB = ND
=> OM = ON => O là trung điểm của MN.
Trong tứ giác AMCN có:
OA = OC, OM = ON
=> Tứ giác AMCN có 2 đường chéo AC và MN cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
khó quá nhỉ
koh lam