K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
20 tháng 4 2017
độ dài đường chéo AC là
\(\sqrt{48^2+36^2}=\sqrt{2304+1296}=\sqrt{3600}=60\)(cm)
vậy độ dài đường chéo AC là 60cm
20 tháng 4 2017
Giải:
Theo định lí Pytago, ta có:
AC2= AD2 +CD2
= 482 + 362
= 2304 + 1296= 3600
AC= 60 (cm)
SG
2
VM
29 tháng 12 2019
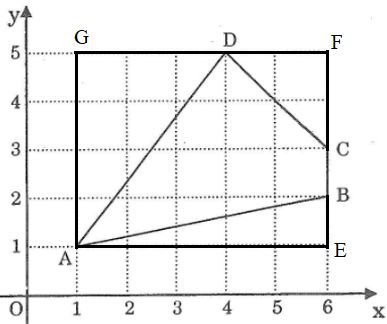
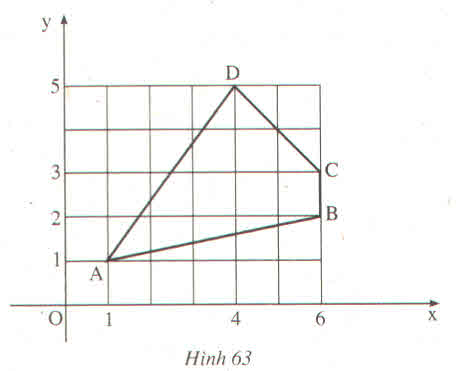
Ta có: \(BC=1.\)
+ Xét \(\Delta ABE\) vuông tại E có:
\(AB^2=AE^2+BE^2\) (định lí Py - ta - go).
=> \(AB^2=5^2+1^2\)
=> \(AB^2=25+1\)
=> \(AB^2=26\)
=> \(AB=\sqrt{26}\) (vì \(AB>0\)).
+ Xét \(\Delta CDF\) vuông tại F có:
\(CD^2=DF^2+CF^2\) (định lí Py - ta - go).
=> \(CD^2=2^2+2^2\)
=> \(CD^2=4+4\)
=> \(CD^2=8\)
=> \(CD=\sqrt{8}\) (vì \(CD>0\)).
+ Xét \(\Delta ADG\) vuông tại G có:
\(AD^2=AG^2+DG^2\) (định lí Py - ta - go).
=> \(AD^2=4^2+3^2\)
=> \(AD^2=16+9\)
=> \(AD^2=25\)
=> \(AD=5\) (vì \(AD>0\)).
Vậy \(AB=\sqrt{26};BC=1;CD=\sqrt{8};AD=5.\)
Chúc bạn học tốt!
MH
26 tháng 5 2017
Ta tính được : AB = \(\sqrt{26}\) ; CD = \(\sqrt{8}\) ; BC = 1 ; DA = 5
13 tháng 5 2017
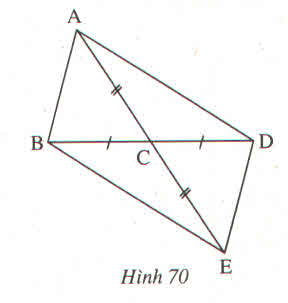
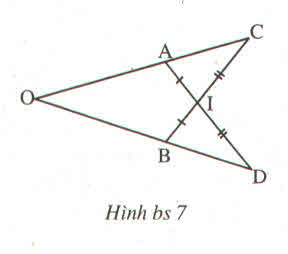
Xét tam giác IAC và IBD có:
IA = IB ( theo đề bài)
Góc AIC = góc BID ( 2 góc đối đỉnh)
IC = ID ( theo đề bài )
Do đó: tam giác IAC = tam giác IBD (c.g.c)
Suy ra góc ACI = góc BDI ( 2 góc tương ứng) \(\left(1\right)\)
Suy ra góc IAC = IBD ( 2góc tương ứng) (*)
Có I nằm giữa B và C
Suy ra: BI + CI = BC (2)
Có I nằm giữa A và D
Suy ra: AI + DI = AD (3)
Từ 2 và 3 suy ra: BC = AD (4)
Có góc OAI + góc IAC = \(180^0\)(2 góc kề bù)
góc OBI + góc IBD = \(180^0\)(2 góc kề bù)
mà: góc IAC = góc IBD (*)
Suy ra góc: OAI = góc OBI (5)
Xét tam giác: OAD và tam giác OBC có:
góc ACI = góc BDI (1)
AD = BC (4)
góc OAI = góc OBI (5)
Do đó: tam giác OAD = tam giác OBC (g.c.g)
Suy ra: OA = OB (2 cạnh tương ứng)
20 tháng 1 2019
Xét tam giác IAC và tam giác IBD có:
IA = IB ( gt)
Góc AIC = góc BID ( 2 góc đối đỉnh)
IC = ID ( gt )
=> Tam giác IAC = tam giác IBD (c.g.c)
=> Góc ACI = góc BDI ( 2 góc tương ứng) (1)
và góc IAC = IBD ( 2góc tương ứng) (*)
Có I nằm giữa B và C
Suy ra: BI + CI = BC (2)
Có I nằm giữa A và D
Suy ra: AI + DI = AD (3)
Từ 2 và 3 suy ra: BC = AD (4)
Có góc OAI + góc IAC = 1800 (2 góc kề bù)
góc OBI + góc IBD = 1800 (2 góc kề bù)
mà: góc IAC = góc IBD (*)
=> góc: OAI = góc OBI (5)
Xét tam giác OAD và tam giác OBC có:
góc ACI = góc BDI (1)
AD = BC (4)
góc OAI = góc OBI (5)
=> Tam giác OAD = tam giác OBC (g.c.g)
=> OA = OB (2 cạnh tương ứng)
LD
12 tháng 3 2018
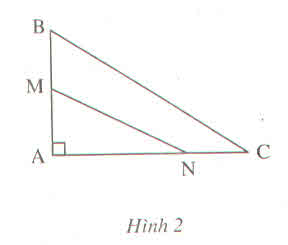
Hình chiếu của AN < hình chiếu của AC
=> đường xiên BN < đường xiên của BC (1)
Hình chiếu của AM < hình chiếu AB => đường xiên MN < đường xiên NB. (2)
Từ (1) và (2) suy ra:
MN< BN< BC.
SG
1
13 tháng 5 2017
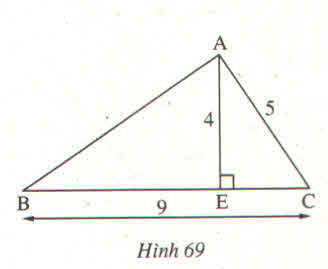
Tam giác AEC có góc AEC = \(90^0\)
=> \(AC^2=AE^2+EC^2\)
=>\(EC^2=AC^2-AE^2\)
=>\(EC^2=5^2-4^2\)
=>\(EC=\sqrt{9}=3\left(m\right)\)
Có EB + EC = BC
=>EB = BC - EC
=>EB = 9 - 3
=> EB = 6 (m)
Tam giác AEB có góc AEB = \(90^0\)
=>\(AB^2=AE^2+EB^2\)
=>\(AB^2=4^2+6^2\)
=>\(AB^2=16+36\)
=>\(AB^2=52\)
=>\(AB=\sqrt{52}=2\sqrt{13}\) (m)
18 tháng 5 2022
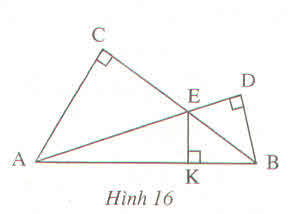
Xét ΔAEB có
AC là đường cao
BD là đường cao
EK là đường cao
Do đó: AC,BD,EK cùng đi qua một điểm
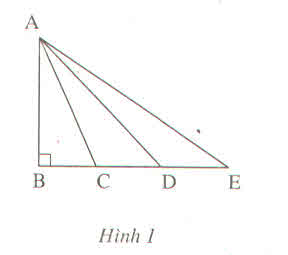
Điểm C nằm giữa B và D nên BC < BD (1)
Điểm C nằm giữa B và E nên BD < BE (2)
Vì B, C, D, E thẳng hàng. Từ (1) và (2) suy ra
BC < BD < BE
AB⊥BE
Suy ra: AB < AC < AD < AE.