K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 5 2021
Đề bài thiếu và sai rất nhiều
1. SA có liên hệ gì với đáy?
2. Đáy là tam giác đều cạnh dài bao nhiêu
3. B thuộc (SBP) nên hiển nhiên khoảng cách từ B đến (SBP) bằng 0, không cần phải tính

CM
4 tháng 1 2018
Chọn A
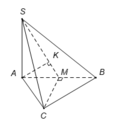
Xác định được
![]()
![]()
Do M là trung điểm của cạnh AB nên
![]()
![]()
![]()
Tam giác vuông SAM có
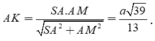
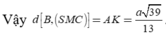


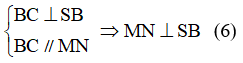



\(BP=\dfrac{1}{3}AB\Rightarrow BP=\dfrac{1}{2}AP\)
\(\Rightarrow d\left(B;\left(SPC\right)\right)=\dfrac{1}{2}d\left(A;\left(SPC\right)\right)\)
Trong tam giác APC, kẻ \(AH\perp CP\Rightarrow CP\left(SAH\right)\)
Trong tam giác vuông SAH, kẻ \(AK\perp SH\Rightarrow AK\perp\left(SPC\right)\Rightarrow AK=d\left(A;\left(SPC\right)\right)\)
\(AP=\dfrac{2}{3}AB=\dfrac{2a}{3}\Rightarrow CP=\sqrt{AP^2+AC^2-2AP.AC.cos60^0}=\dfrac{a\sqrt{7}}{3}\)
Áp dụng định lý hàm sin:
\(\dfrac{AP}{sin\widehat{ACP}}=\dfrac{CP}{sinA}\Rightarrow sin\widehat{ACP}=\dfrac{AP.sin60^0}{CP}=\dfrac{\sqrt{21}}{7}\)
\(\Rightarrow AH=AC.sin\widehat{ACP}=\dfrac{a\sqrt{21}}{7}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}\Rightarrow AK=\dfrac{SA.AH}{\sqrt{SA^2+AH^2}}=\dfrac{2a\sqrt{93}}{31}\)
\(\Rightarrow d\left(B;\left(SPC\right)\right)=\dfrac{1}{2}AK=\dfrac{a\sqrt{93}}{31}\)
Bạn kiểm tra lại phần tính toán