K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

MH
22 tháng 4 2017
Từ x1 < x2 và 3 > 0
suy ra : 3x1< 3x2 hay f(x1) < f(x2 ).
Vậy hàm số đã cho đồng biến trên R.

LH
22 tháng 4 2017
a) Hàm số nghịch biến trên R vì 1 - \(\sqrt{ }\)5 < 0.
b) Khi x = 1 + \(\sqrt{ }\)5 thì y = -5.
c) Khi y = \(\sqrt{ }\)5 thì x = \(\dfrac{-3+\sqrt{5}}{2}\)
22 tháng 4 2017
Bài giải:
a) Hàm số nghịch biến trên R vì 1 - √5 < 0.
b) Khi x = 1 + √5 thì y = -5.
c) Khi y = √5 thì x = -3+√523+52.

2 tháng 5 2017
a, \(\left\{{}\begin{matrix}m\ge0\\\sqrt{m}\ne\sqrt{5}\Leftrightarrow m\ne5\end{matrix}\right.\)
b, Để là hàm số đồng biến thì:\(\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}>0\Rightarrow\sqrt{m}+\sqrt{5}>0\Leftrightarrow m>5\)

2 tháng 10 2020
Sửa đề bài ( thêm ) . Tìm tất cả các hàm \(f:ℝ\rightarrowℝ\)

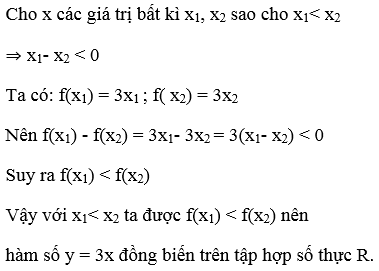
Cho hàm số : \(y=f\left(x\right)=\dfrac{2}{3}x+5\) với \(x\in R\)
Giả sử : \(x_1< x_2\)
\(f\left(x_1\right)=\dfrac{2}{3}x_1+5\)
\(f\left(x_2\right)=\dfrac{2}{3}x_2+5\)
Từ \(x_1< x_2\) \(\Rightarrow\dfrac{2}{3}x_1< \dfrac{2}{3}x_2\)
\(\Rightarrow\dfrac{2}{3}x_1+5< \dfrac{2}{3}x_2+5\)
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
Vậy hàm số đồng biến trên \(R\)