Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
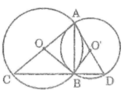
Tam giác ABC nội tiếp trong đường tròn (O) có AC là đường kính nên góc (ABC) = 90 °
Tam giác ABD nội tiếp trong đường tròn (O’) có AD là đường kính nên góc (ABD) = 90 °
Ta có: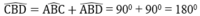
Vậy ba điểm C, B, D thẳng hàng và AB ⊥ CD
a: góc ABC=1/2*sđ cung AC=90 độ
góc ABD=1/2*180=90 độ
góc CBD=góc ABC+góc ABD=90+90=180 độ
=>C,B,D thẳng hàng
b: góc AFC=1/2*sđ cung AC=90 độ
=>CF vuông góc AD
góc AED=1/2*180=90 độ
=>DE vuông góc AC
góc CED=góc CFD=90 độ
=>CEFD nội tiếp
Vì góc ACB là có nội tiếp chắn nửa đường tròn của (O)
=> góc ACB= 90 độ
Xét (I) có góc MCN là góc nội tiếp chắn cung MN
mà góc MCN= 90 độ
=> MN là đường kính của (I)
=> 3 điểm M,I,N thẳng hàng
b) vì Δ CIN cân tại I( IC=IN=R)
=> góc ICN= góc INC
lại có Δ COB cân tại O(OC=OB=R)
=> góc OCB= góc OBC
=> góc INC= góc OBC ( cùng = góc OCB)
mà 2 góc này ở vị trí đồng vị của 2 đường thẳng MN và AB
=> MN // AB
lại có ID vuông góc với AB
=> ID vuông góc với MN( đpcm)
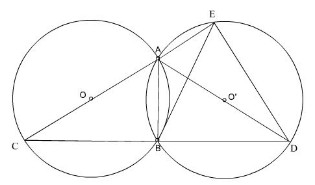
a) Nối C đến D.
Ta có 2 đường tròn bằng nhau => AC = AD
=> ∆ ACD cân tại A
Lại có góc ABC = 90°; do có OB = OC = OA = R ( tính chất trung tuyến ứng với cạnh huyền )
Tương tự có góc ABD = 90°
=> ABC + ABD = 180°
=> C; B; D thẳng hàng và AB ⊥ CD
=> BC = BD
=> cung BC = cung BD
b) Nối E đến D; từ B hạ BH ⊥ ED Ta có góc DEA = 90° ( chứng minh tương tự theo (a) )
=> BH // EC
Mà theo (a) ta có BE = BD
=> BH là đường trung bình tam giác CDE
=> HE = HD mà BH ⊥ ED => B là điểm chính giữa cung EBD
Nối B với 3 điểm A, C, D ta có:
=
(góc nội tiếp chắn nửa đường tròn)
=
( góc nội tiếp chắn nửa đường tròn)
Vậy +
=
Suy ra ba điểm A, C, D thẳng hàng.
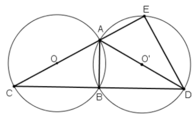
Xét tam giác AED có đường trung tuyến EO' bằng một phần hai cạnh tương ứng là AD ( O'E = O'A = O'D = AD/2)
=> Tam giác AED vuông tại E
⇒ 
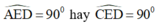
⇒ ΔECD vuông tại E.
Tam giác ECD vuông có EB là đường trung tuyến ứng với cạnh huyền( Vì BC = BD câu (a) )
⇒ EB = BD (CD/2).
⇒ 
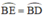(định lý) hay B là điểm chính giữa cung 
