Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BHCD có
CH//BD
BH//CD
Do đó: BHCD là hình bình hành

a: Xet ΔABC và ΔEBA có
góc BAC=góc BEA
góc B chung
=>ΔABC đồng dạng với ΔEBA
b: ΔABC vuông tại A có AE vuông góc BC
nên AB^2=BE*BC
c: BF là phân giác
=>AF/AB=CF/BC
=>AF/3=FC/5=4/8=1/2
=>AF=1,5cm

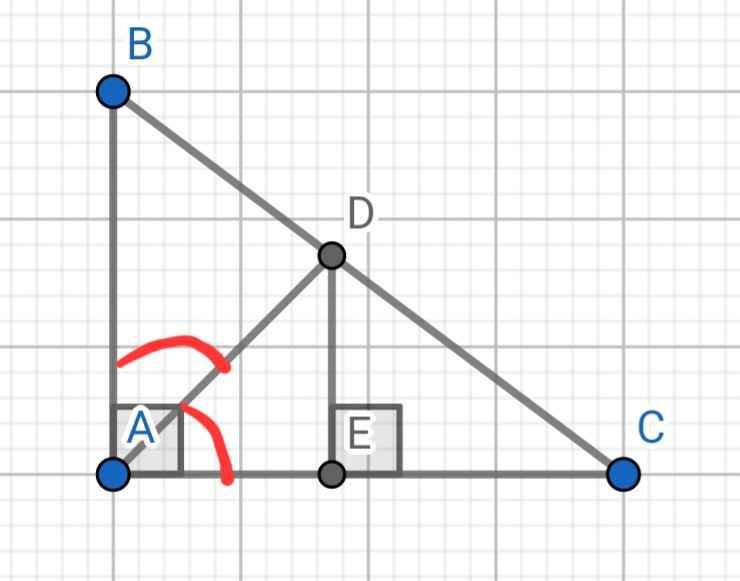
a) Do AD là đường phân giác của ∠BAC
⇒ BD/CD = AB/AC = 9/12 = 3/4
b) Xét hai tam giác vuông: ∆ABC và ∆EDC có:
∠C chung
⇒ ∆ABC ∽ ∆EDC (g-g)
a: BD/CD=AB/AC=3/4
b: Xét ΔABC vuông tại A và ΔEDC vuông tại E có
góc C chung
=>ΔABC đồng dạng với ΔEDC

a, Nửa chu vi là \(\frac{6+6+6}{2}=9cm\)
Diện tích tam giác là \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{9\left(9-6\right)\left(9-6\right)\left(9-6\right)}\)
\(=\sqrt{9.3.3.3}=9\sqrt{3}\)cm2
b, Xét tam giác ABC vuông tại A
tan^B = \(\frac{AC}{AB}\Rightarrow\frac{\sqrt{3}}{3}=\frac{2}{AB}\Rightarrow AB=\frac{6\sqrt{3}}{3}=2\sqrt{3}\)cm
Diện tích tam giác là \(\frac{1}{2}AB.AC=6\sqrt{3}\)cm2
c, Dựng AH là đường cao đồng thời là đường trung tuyến do tam giác ABC cân tại A
=> HC = BC/2 = 3 cm
Theo định lí Pytago tam giác AHC vuông tại H
\(AH=\sqrt{AC^2-HC^2}=4cm\)
Diện tích tam giác ABC là : \(\frac{1}{2}AH.BC=\frac{4.6}{2}=12cm^2\)
Xét tam giác ABC có:
\(AD=12,5=\dfrac{BC}{2}\)
=> Tam giác ABC vuông tại A
=> \(AC^2=BC^2-AB^2=25^2-7^2=576\)( định lý Pytago)
\(\Rightarrow AC=24\)
\(\Delta ABC\) có \(AD=\dfrac{1}{2}BC\left(12,5=\dfrac{1}{2}\cdot25\right)\) nên là tam giác vuông tại A
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=24\left(pytago\right)\)