Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BHCD có
CH//BD
BH//CD
Do đó: BHCD là hình bình hành

a: Xét tứ giác BHCD có
BH//CD
CH//BD
Do đó: BHCD là hình bình hành

Cho hình thoi 𝐴𝐵𝐶𝐷 (𝐴መ > 90). Gọi 𝐸 là hình chiếu vuông góc của 𝐴 trên 𝐵𝐶, 𝐹 là hình
chiếu vuông góc của 𝐶 trên 𝐴𝐷.
a) Tứ giác 𝐴𝐸𝐶𝐹 là hình gì? Vì sao?
b) 𝐵𝐷 cắt 𝐴𝐸 tại 𝐻, cắt 𝐶𝐹 tại 𝐾. Chứng minh rằng 𝐴𝐾 = 𝐶𝐻.
c) Gọi 𝐼 là giao điểm của 𝐴𝐾 và 𝐶𝐷, 𝐽 là giao điểm của 𝐶𝐻 và 𝐴𝐵. Chứng minh rằng 𝐸𝐼 ⊥ 𝐸𝐽

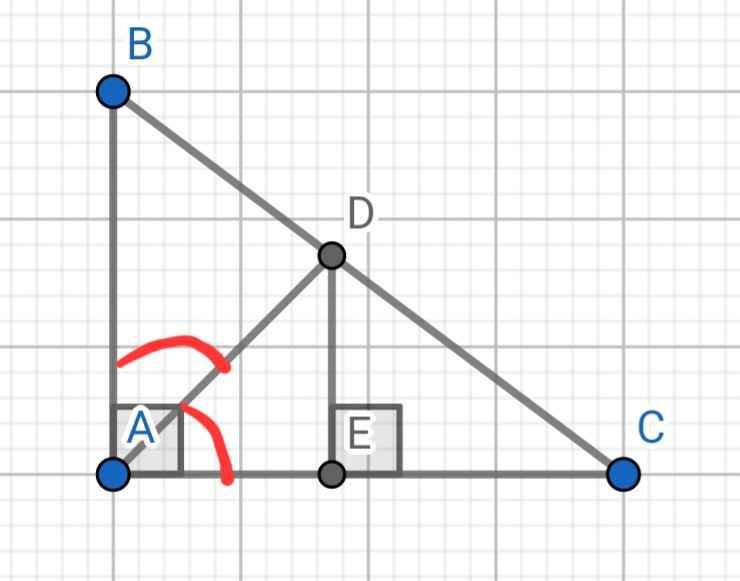
a) Do AD là đường phân giác của ∠BAC
⇒ BD/CD = AB/AC = 9/12 = 3/4
b) Xét hai tam giác vuông: ∆ABC và ∆EDC có:
∠C chung
⇒ ∆ABC ∽ ∆EDC (g-g)
a: BD/CD=AB/AC=3/4
b: Xét ΔABC vuông tại A và ΔEDC vuông tại E có
góc C chung
=>ΔABC đồng dạng với ΔEDC

a: Ta có: \(A=-x^2+2x+5\)
\(=-\left(x^2-2x-5\right)\)
\(=-\left(x^2-2x+1-6\right)\)
\(=-\left(x-1\right)^2+6\le6\forall x\)
Dấu '=' xảy ra khi x=1
b: Ta có: \(B=-x^2-8x+10\)
\(=-\left(x^2+8x-10\right)\)
\(=-\left(x^2+8x+16-26\right)\)
\(=-\left(x+4\right)^2+26\le26\forall x\)
Dấu '=' xảy ra khi x=-4
c: Ta có: \(C=-3x^2+12x+8\)
\(=-3\left(x^2-4x-\dfrac{8}{3}\right)\)
\(=-3\left(x^2-4x+4-\dfrac{20}{3}\right)\)
\(=-3\left(x-2\right)^2+20\le20\forall x\)
Dấu '=' xảy ra khi x=2
d: Ta có: \(D=-5x^2+9x-3\)
\(=-5\left(x^2-\dfrac{9}{5}x+\dfrac{3}{5}\right)\)
\(=-5\left(x^2-2\cdot x\cdot\dfrac{9}{10}+\dfrac{81}{100}-\dfrac{21}{100}\right)\)
\(=-5\left(x-\dfrac{9}{10}\right)^2+\dfrac{21}{20}\le\dfrac{21}{20}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{9}{10}\)
e: Ta có: \(E=\left(4-x\right)\left(x+6\right)\)
\(=4x+24-x^2-6x\)
\(=-x^2-2x+24\)
\(=-\left(x^2+2x-24\right)\)
\(=-\left(x^2+2x+1-25\right)\)
\(=-\left(x+1\right)^2+25\le25\forall x\)
Dấu '=' xảy ra khi x=-1
f: Ta có: \(F=\left(2x+5\right)\left(4-3x\right)\)
\(=8x-6x^2+20-15x\)
\(=-6x^2-7x+20\)
\(=-6\left(x^2+\dfrac{7}{6}x-\dfrac{10}{3}\right)\)
\(=-6\left(x^2+2\cdot x\cdot\dfrac{7}{12}+\dfrac{49}{144}-\dfrac{529}{144}\right)\)
\(=-6\left(x+\dfrac{7}{12}\right)^2+\dfrac{529}{24}\le\dfrac{529}{24}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{7}{12}\)