Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. ĐKXĐ: \(x\ne\pm1\)
2. \(A=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right)\cdot\dfrac{x+1}{2}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{x^2+2x+1-x^2+4x-3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{6x-2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{2\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x-3}{x-1}\)
3. Tại x = 5, A có giá trị là:
\(\dfrac{5-3}{5-1}=\dfrac{1}{2}\)
4. \(A=\dfrac{x-3}{x-1}\) \(=\dfrac{x-1-3}{x-1}=1-\dfrac{3}{x-1}\)
Để A nguyên => \(3⋮\left(x-1\right)\) hay \(\left(x-1\right)\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\left(tmđk\right)\\x=0\left(tmđk\right)\\x=4\left(tmđk\right)\\x=-2\left(tmđk\right)\end{matrix}\right.\)
Vậy: A nguyên khi \(x=\left\{2;0;4;-2\right\}\)

a) ĐKXĐ: \(x\ne-3,x\ne2\)
b) \(A=\dfrac{\left(x-2\right)\left(x+2\right)-5-\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}=\dfrac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}=\dfrac{\left(x+3\right)\left(x-4\right)}{\left(x+3\right)\left(x-2\right)}=\dfrac{x-4}{x-2}\)
c) \(A=\dfrac{x-4}{x-2}=\dfrac{3-4}{3-2}=-1\)

Bài 2
a) ĐKXĐ: x - 10 0 và x + 10 0
*) x - 10 0
x 10
*) x + 10 0
x 10
Vậy ĐKXĐ: x -10; x 10
b) P = [(5x + 2)(x + 10) + (5x - 2)(x - 10)]/[(x - 10)(x + 10)] . (x - 10)/(x² + 4)
= (5x² + 50x + 2x + 20 + 5x² - 50x - 2x + 20)/[(x + 10)(x² + 4)]
= (10x² + 40)/[(x + 10)(x² + 4)]
= 10(x² + 4)/[(x + 10)(x² + 4)]
= 10/(x + 10)
c) Khi x = 2/5 ta có:
P = 10.(2/5 + 10)
= 4 + 100
= 104

Đề bài là \(B=\dfrac{\left(x-1\right)^2-4}{\left(2x+1\right)^2-\left(x+2\right)^2}\) hay là \(B=\dfrac{\left(x-1\right)^2-4}{\left(2x+1\right)^2}-\left(x+2\right)^2?\)
\(\dfrac{\left(x-1\right)^2-4}{\left(2x+1\right)^2-\left(x+2\right)^2}\)
viết lại biểu thức

a: \(A=\left(\dfrac{x}{x^2-4}+\dfrac{4}{x-2}+\dfrac{1}{x+2}\right):\dfrac{3x+3}{x^2+2x}\)
\(=\dfrac{x+4x+8+x-2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x+2\right)}{3\left(x+1\right)}\)
\(=\dfrac{6\left(x+1\right)\cdot x\left(x+2\right)}{3\left(x+1\right)\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{x-2}\)

a: ĐKXĐ: x<>0; x<>-3
b: \(=\dfrac{x^2+6x+9}{x\left(x+3\right)}\cdot\dfrac{2}{x+3}=\dfrac{2}{x}\)
c: Khi x=1/5 thì A=2:1/5=10

Bài 1: ĐKXĐ:`x + 3 ne 0` và `x^2+ x-6 ne 0 ; 2-x ne 0`
`<=> x ne -3 ; (x-2)(x+3) ne 0 ; x ne2`
`<=>x ne -3 ; x ne 2`
b) Với `x ne - 3 ; x ne 2` ta có:
`P= (x+2)/(x+3) - 5/(x^2 +x -6) + 1/(2-x)`
`P = (x+2)/(x+3) - 5/[(x-2)(x+3)] + 1/(2-x)`
`= [(x+2)(x-2)]/[(x-2)(x+3)] - 5/[(x-2)(x+3)] - (x+3)/[(x-2)(x+3)]`
`= (x^2 -4)/[(x-2)(x+3)] - 5/[(x-2)(x+3)] - (x+3)/[(x-2)(x+3)]`
`=(x^2 - 4 - 5 - x-3)/[(x-2)(x+3)]`
`= (x^2 - x-12)/[(x-2)(x+3)]`
`= [(x-4)(x+3)]/[(x-2)(x+3)]`
`= (x-4)/(x-2)`
Vậy `P= (x-4)/(x-2)` với `x ne -3 ; x ne 2`
c) Để `P = -3/4`
`=> (x-4)/(x-2) = -3/4`
`=> 4(x-4) = -3(x-2)`
`<=>4x -16 = -3x + 6`
`<=> 4x + 3x = 6 + 16`
`<=> 7x = 22`
`<=> x= 22/7` (thỏa mãn ĐKXĐ)
Vậy `x = 22/7` thì `P = -3/4`
d) Ta có: `P= (x-4)/(x-2)`
`P= (x-2-2)/(x-2)`
`P= 1 - 2/(x-2)`
Để P nguyên thì `2/(x-2)` nguyên
`=> 2 vdots x-2`
`=> x -2 in Ư(2) ={ 1 ;2 ;-1;-2}`
+) Với `x -2 =1 => x= 3` (thỏa mãn ĐKXĐ)
+) Với `x -2 =2 => x= 4` (thỏa mãn ĐKXĐ)
+) Với `x -2 = -1=> x= 1` (thỏa mãn ĐKXĐ)
+) Với `x -2 = -2 => x= 0`(thỏa mãn ĐKXĐ)
Vậy `x in{ 3 ;4; 1; 0}` thì `P` nguyên
e) Từ `x^2 -9 =0`
`<=> (x-3)(x+3)=0`
`<=> x= 3` hoặc `x= -3`
+) Với `x=3` (thỏa mãn ĐKXĐ) thì:
`P = (3-4)/(3-2)`
`P= -1/1`
`P=-1`
+) Với `x= -3` thì không thỏa mãn ĐKXĐ
Vậy với x= 3 thì `P= -1`

a) ĐKXĐ: \(x\ne\pm10\)
b) \(P=\left(\dfrac{5x+2}{x-10}+\dfrac{5x-2}{x+10}\right)\cdot\dfrac{x-10}{x^2+4}\left(x\ne\pm10\right)\)
\(=\left[\dfrac{\left(5x+2\right)\left(x+10\right)}{\left(x-10\right)\left(x+10\right)}+\dfrac{\left(5x-2\right)\left(x-10\right)}{\left(x-10\right)\left(x+10\right)}\right]\cdot\dfrac{x-10}{x^2+4}\)
\(=\dfrac{5x^2+52x+20+5x^2-52x+20}{\left(x-10\right)\left(x+10\right)}\cdot\dfrac{x-10}{x^2+4}\)
\(=\dfrac{10x^2+40}{x+10}\cdot\dfrac{1}{x^2+4}\)
\(=\dfrac{10\left(x^2+4\right)}{\left(x+10\right)\left(x^2+4\right)}\)
\(=\dfrac{10}{x+10}\)
c) Thay \(x=\dfrac{2}{5}\) vào \(P\), ta được:
\(P=\dfrac{10}{\dfrac{2}{5}+10}=\dfrac{25}{26}\)
\(\text{#}Toru\)


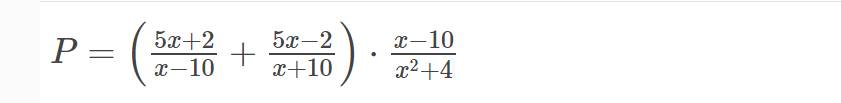
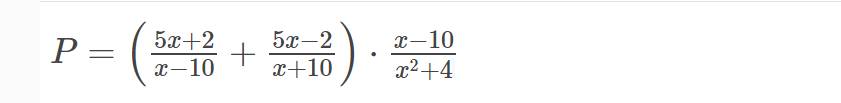
đkxđ:\(x\ne5,x\ne-5\)
\(\dfrac{2x}{\left(x-5\right)\left(x+5\right)}-\dfrac{5}{x-5}-\dfrac{1}{x+5}\)
\(\dfrac{2x}{\left(x-5\right)\left(x+5\right)}-\dfrac{5x+25}{\left(x-5\right)\left(x+5\right)}-\dfrac{x-5}{\left(x-5\right)\left(x+5\right)}\)
\(\dfrac{2x-5x-25-x+5}{\left(x-5\right)\left(x+5\right)}=\dfrac{-4x-20}{\left(x-5\right)\left(x+5\right)}=\dfrac{-4\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}=-\dfrac{4}{x-5}\)
thay x=1 vào bt A, ta được:
\(-\dfrac{4}{1-5}=1\)