Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



biết là sử dụng BĐT này rùi thì áp dụng mà giải hỏi làm chi :D

A B C K H I
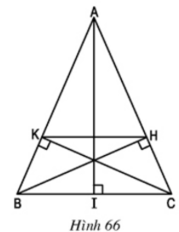
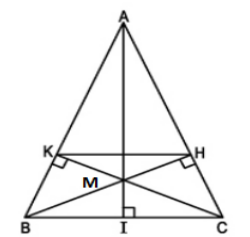
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)

a) Tự áp dụng tính chất dãy tỉ số bằng nhau ta có :
A = 120°
B = 100°
C = 80°
D = 60°
b) Xét tứ giác ABCD có :
A + B + C + D = 360°
=> A = 360° - 60° - 120° - 80°= 100°
Góc ngoài tại A :
180° - 100° = 80°
c) Tổng quát :
Gọi góc ngoài tại A là HAD
Góc ngoài tại D là ADE
Góc ngoài tại B là CBG
Góc ngoài tại C là BCM
Ta có :
HAD = 180° - DAB
ADE = 180° ADC
CBG = 180° - ABC
BCM = 180° - BCD
=> HAD + ADE + CBG + BCM =
( 180° - DAB ) + ( 180° - ADC ) + ( 180° - ABC ) + ( 180° - BCD )
= ( 180° + 180° + 180° + 180°) - ( DAB + ACD + ABC + BCD )
= 720° - 360°
= 360°
=> Tổng các góc ngoài = 360°
d ) Nếu các góc trong tứ giác \(\le\)90°
=> Tổng 4 góc trong tứ giác đó sẽ \(\le\)360°
=> Không tồn tại tứ giác đều là góc nhọn
Nếu các góc trong tứ giác \(\ge\)90°
=> Tổng các góc trong tứ giác đó \(\ge\)360°
=> Không tồn tại tứ giác đều là góc tù

Đề thiếu \(0\le a,b,c\le\dfrac{4}{3}\)
\(b+c=2-a\)
\(bc=1-a\left(b+c\right)=1-a\left(2-a\right)=1-2a+a^2\)
Áp dụng BĐT \(\left(x+y\right)^2\ge4xy\), ta có
\(\left(2-a\right)^2\ge4\left(1-2a+a^2\right)\)
\(4-4a+a^2\ge4-8a+4a^2\)
\(4-4a+a^2-4+8a-4a^2\ge0\)
\(-3a^2+4a\ge0\)
\(3a^2-4a\le0\)
\(a\left(3a-4\right)\le0\)
\(\Rightarrow0\le a\le\dfrac{4}{3}\)
Tương tự với b,c


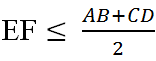







 = 6 : 5 : 4 : 3. Tính các góc của tứ giác ABCD.
= 6 : 5 : 4 : 3. Tính các góc của tứ giác ABCD. = 600,
= 600,  = 1200,
= 1200,  = 800. Tính số đo góc ngoài tại đỉnh A.
= 800. Tính số đo góc ngoài tại đỉnh A. a,b,c
a,b,c
Vì a>0; b>0 nên a + b \geq 4ab1+ab4ab1+ab
\Leftrightarrow (a + b)(1 + ab)\geq 4ab
\Leftrightarrow a + b + a^2b+ab^2\geq 4ab
\Leftrightarrow a + b + a^b + ab^2 - 4ab\geq 0
\Leftrightarrow (a^2b - 2ab + b) + (ab^2 - 2ab +a) \geq 0
\Leftrightarrow b(a^2 -2a + 1) + a(b^2 - 2B + 1)\geq 0
\Leftrightarrow b(a-1)^2 + a(b-1)^2\geq 0
\Rightarrow Bất đẳng thức đúng\Rightarrow đpcm.
Vì a,b > 0 =) ab > 0
Áp dụng BĐT Côsi cho hai số a,b không âm ta có :
\(\frac{a+b}{2}\ge\sqrt{ab}\)
\(\Rightarrow a+b\ge2\sqrt{ab}\)
Áp dụng BĐT Côsi cho hai số 1 , ab không âm ta có :
\(\frac{1+ab}{2}\ge\sqrt{ab}\)
\(\Rightarrow1+ab\ge2\sqrt{ab}\)
Ta có :
\(\frac{4ab}{1+ab}\le\frac{4ab}{2\sqrt{ab}}\)(Vì \(1+ab\ge2\sqrt{ab}\))
mà \(\frac{4ab}{2\sqrt{ab}}=2\sqrt{ab}\)
\(\Rightarrow\frac{4ab}{1+ab}\le2\sqrt{ab}\)(1)
Lại có : \(a+b\ge2\sqrt{ab}\)(2)
Từ (1) và (2) \(\Rightarrow a+b\ge\frac{4ab}{1+ab}\)
Chúc bạn học tốt =))