Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a,b,c 
thành tích
chia hết cho 4
b. 
d. 
b. 
d. 
g. 
b. 
d. 
Bài 1: (4n + 3 )2 -25 = ( 4n+ 3 - 5 ) ( 4n + 3 + 5 ) = ( 4n - 2 ) ( 4n + 8 )
=> ( 4n - 2 ) ( 4n + 8 ) chia hết cho 8 với \(\forall n\)
=> (4n+3)2 - 25 chia hết cho 8 với mọi n
Bài 2: (2n + 3)2 - 9 = ( 2n + 3 + 3 ) ( 2n+3-3) = (2n+6) . 2n = 4n2 +6 chia hết cho 4 với \(\forall n\)
Vậy (2n+3)2 - 9 chia hết cho 4 với mọi n
Bài 3: m2 - n2 = ( m - n ) ( m + n )
b) -16 + (x-3)2 = (x-3)2 -16 = ( x - 3 -4 ) ( x-3+4 ) = (x - 7 ) ( x +1 )
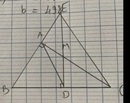
A B C H I M N K
do từ câu b ta có MHNK là hình vuông từ đó ta có
MN là trung trực của KH (1)
mà ta có hai tam giác vuông IKB và IHB nên ta có \(PH=PK=\frac{1}{2}BI\)( đường trung tuyến ứng với cạnh huyền)
Do PH=PK nên P thuộc đường trung trực của KH (2)
từ (1) và (2) ta có P thuộc MN
chứng minh tương tự ta có
Q thuộc MN
do đó M,N,P,Q thẳng hàng
các điểm lưới (cách đều nhau) trong hình vuông được hiển thị trong sơ đồ dưới đây, bao gồm các điểm trên các cạnh. Điểm 
nằm ở trung tâm của hình vuông. Cho rằng điểm đó 
được chọn ngẫu nhiên trong số các 
điểm khác , xác suất để đường thẳng đó 
là đường đối xứng với hình vuông là bao nhiêu?
Đề thiếu \(0\le a,b,c\le\dfrac{4}{3}\)
\(b+c=2-a\)
\(bc=1-a\left(b+c\right)=1-a\left(2-a\right)=1-2a+a^2\)
Áp dụng BĐT \(\left(x+y\right)^2\ge4xy\), ta có
\(\left(2-a\right)^2\ge4\left(1-2a+a^2\right)\)
\(4-4a+a^2\ge4-8a+4a^2\)
\(4-4a+a^2-4+8a-4a^2\ge0\)
\(-3a^2+4a\ge0\)
\(3a^2-4a\le0\)
\(a\left(3a-4\right)\le0\)
\(\Rightarrow0\le a\le\dfrac{4}{3}\)
Tương tự với b,c
cảm ơn ạ!