K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TQ
2
17 tháng 2 2017
Vì a>0; b>0 nên a + b \geq 4ab1+ab4ab1+ab
\Leftrightarrow (a + b)(1 + ab)\geq 4ab
\Leftrightarrow a + b + a^2b+ab^2\geq 4ab
\Leftrightarrow a + b + a^b + ab^2 - 4ab\geq 0
\Leftrightarrow (a^2b - 2ab + b) + (ab^2 - 2ab +a) \geq 0
\Leftrightarrow b(a^2 -2a + 1) + a(b^2 - 2B + 1)\geq 0
\Leftrightarrow b(a-1)^2 + a(b-1)^2\geq 0
\Rightarrow Bất đẳng thức đúng\Rightarrow đpcm.
PC
17 tháng 2 2017
Vì a,b > 0 =) ab > 0
Áp dụng BĐT Côsi cho hai số a,b không âm ta có :
\(\frac{a+b}{2}\ge\sqrt{ab}\)
\(\Rightarrow a+b\ge2\sqrt{ab}\)
Áp dụng BĐT Côsi cho hai số 1 , ab không âm ta có :
\(\frac{1+ab}{2}\ge\sqrt{ab}\)
\(\Rightarrow1+ab\ge2\sqrt{ab}\)
Ta có :
\(\frac{4ab}{1+ab}\le\frac{4ab}{2\sqrt{ab}}\)(Vì \(1+ab\ge2\sqrt{ab}\))
mà \(\frac{4ab}{2\sqrt{ab}}=2\sqrt{ab}\)
\(\Rightarrow\frac{4ab}{1+ab}\le2\sqrt{ab}\)(1)
Lại có : \(a+b\ge2\sqrt{ab}\)(2)
Từ (1) và (2) \(\Rightarrow a+b\ge\frac{4ab}{1+ab}\)
Chúc bạn học tốt =))
thành tích
chia hết cho 4
b. 
d. 
b. 
d. 
g. 
b. 
d. 
HN
20 tháng 9 2017
Bài 1: (4n + 3 )2 -25 = ( 4n+ 3 - 5 ) ( 4n + 3 + 5 ) = ( 4n - 2 ) ( 4n + 8 )
=> ( 4n - 2 ) ( 4n + 8 ) chia hết cho 8 với \(\forall n\)
=> (4n+3)2 - 25 chia hết cho 8 với mọi n
Bài 2: (2n + 3)2 - 9 = ( 2n + 3 + 3 ) ( 2n+3-3) = (2n+6) . 2n = 4n2 +6 chia hết cho 4 với \(\forall n\)
Vậy (2n+3)2 - 9 chia hết cho 4 với mọi n
Bài 3: m2 - n2 = ( m - n ) ( m + n )
b) -16 + (x-3)2 = (x-3)2 -16 = ( x - 3 -4 ) ( x-3+4 ) = (x - 7 ) ( x +1 )
MN
30 tháng 6 2021
a) xét tam giác ABC và tam giác DBE : gốc B chung, góc A = góc D (=90) => hai tam giác đồng dang theo trường hợp góc góc
b) xét tam giác MAE và tam giác MDC : A=D (=90); góc AME= góc DMC ( doi dinh) => hai tam giác đồng dang theo trường hợp góc góc => MA/MD=ME/MC ( ti so đồng dang) => đpcm
c) ta có: MA/MD=ME/MC =-> MA/ME=MD/MC+ góc AMD=góc EMC => tam giac MAD dong dang tam giac MEC
d) tam giac ABC dong dang tam giác AME (g-g). : A =A(=90); góc ACB = AEM ( cùng phụ góc B)=> AB/AM=AC/AE=> đpcm
.
.
29 tháng 5 2022
Sửa đề: Cho hình bình hành ABCD
Xét tứ giác DBEC có
BE//DC
BE=DC
DO đó: DBEC là hình bình hành
Suy ra: DB//CE và DB=CE
Xét tứ giác BDFC có
BC//DF
BC=DF
Do đó: BDFC là hình bình hành
Suy ra: BD//CF và BD=CF
Ta có: BD//CF
BD//CE
CF và CE có điểm chung là C
Do đó: F,C,E thẳng hàng
mà CE=CF(=BD)
nên C la trung điểm của FE
hay F và E đối xứng nhau qua C
các điểm lưới (cách đều nhau) trong hình vuông được hiển thị trong sơ đồ dưới đây, bao gồm các điểm trên các cạnh. Điểm 
nằm ở trung tâm của hình vuông. Cho rằng điểm đó 
được chọn ngẫu nhiên trong số các 
điểm khác , xác suất để đường thẳng đó 
là đường đối xứng với hình vuông là bao nhiêu?
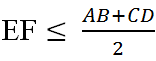
thếu đề