Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(A=20x^3-10x^2+5x-20x^3+10x^2+4x=9x\)
Thay x = 15 vào bt A ta có
A = 9 . 15 = 135
b/ \(B=5x^2-20xy-4y^2+2xy=5x^2-4y^2\)
Thay x = -1/5 ; y = - 1/2 vào bt B ta có
\(B=5.\dfrac{1}{25}-4.\dfrac{1}{4}=\dfrac{1}{5}-1=-\dfrac{4}{5}\)
c/ \(C=6x^2y^2-6xy^3-8x^3+8x^2y^2-5x^2y^2+5xy^3\)
\(=9x^2y^2-xy^3-8x^3\)
Thay x = 1/2 ; y = 2 vào bt C ta có
\(C=9.4.\dfrac{1}{4}-\dfrac{1}{2}.8-8.\dfrac{1}{8}=9-4-1=4\)
d/ \(D=6x^2+10x-3x-5+6x^2-3x+8x-2\)
\(=12x^2+12x-3\)
\(\left|x\right|=2\Rightarrow x=\pm2\)
Thay x = 2 vào bt D có
\(D=12.4+12.2-3=69\)
Thay x = - 2 vào bt D ta có
\(D=12.4-12.2-3=21\)

Lời giải:
a.
$A=20x^3-10x^2+5x-(20x^3-10x^2-4x)$
$=9x=9.15=135$
b.
$B=(5x^2-20xy)-(4y^2-20xy)=5x^2-4y^2$
$=5(\frac{-1}{5})^2-4(\frac{-1}{2})^2=\frac{-4}{5}$
c.
$C=(6x^2y^2-6xy^3)-(8x^3-8x^2y^2)-(5x^2y^2-5xy^3)$
$=-8x^3+9x^2y^2-xy^3$
$=(-2x)^3+(3xy)^2-xy^3$
$=(-2.\frac{1}{2})^3+(3.\frac{1}{2}.2)^2-\frac{1}{2}.2^3$
$=(-1)^3+3^2-4=4$

c.
C=6(xy)^2-6(xy)y^2-(2x)^3+8(xy)^2+5(xy)^2-5(xy).y^2
C=(6+8+5)(xy)^2-(6+5)(xy)^2.y^2 -(2x)^3+8.(xy)^2
x.y=1; 2x=1
C=19-11.4-1+8
C=26-44=30-40-4-4=-10-8=-18
a)
<=>A=3x[10x^2-2x+1-2(5x^2-x-2)]=3x(1+4)
=3.5.x
x=15
A=3.5.15=15^2=(4^2-1).15=4.15.4-15=60.4-15
=240-15=225

\(A=5x\left(4x^2-2x+1\right)-2x\left(10x^2-5x-2\right)\)
\(=20x^3-10x^2+5x-20x^3+10x^2+4x\)
\(=9x\)
Thay x=15 \(\Rightarrow A=9.15=135\)
\(B=6xy\left(xy-y^2\right)-8x^2\left(x-y^2\right)+5y^2\left(x^2-xy\right)\)
\(=6x^2y^2-6xy^3-8x^3+8x^2y^2+5x^2y^2-5xy^3\)
\(=19x^2y^2-11xy^3-8x^3\)
Thay x=1/2 ; y=2 vào B \(\Rightarrow19.\left(\frac{1}{2}\right)^2.2^2-11\cdot\frac{1}{2}\cdot2^3-8\cdot\left(\frac{1}{2}\right)^3\)
\(=19-44-1\)
\(=-26\)

Bài 1 :
a, \(\left(x^2-2x+3\right)\left(x-4\right)=0\)
TH1 : \(x^2-2x+3=0\)
\(\left(-2\right)^2-4.3=4-12< 0\)vô nghiệm
TH2 : \(x-4=0\Leftrightarrow x=4\)
b, \(\left(2x^2-3x-1\right)\left(5x+2\right)=0\)
TH1 : \(\left(-3\right)^2-4.\left(-1\right).2=9+8=17>0\)
\(\Rightarrow x_1=\frac{3-\sqrt{17}}{4};x_2=\frac{3+\sqrt{17}}{4}\)
TH2 ; \(5x+2=0\Leftrightarrow x=-\frac{2}{5}\)
c, đưa về hệ đc ko ?
d, \(\left(5x^3-x^2+2x-3\right)\left(4x^2-x+2\right)=0\)
TH1 : \(x=0,74...\) ( bấm máy cx ra )
TH2 : \(\left(-1\right)^2-4.2.4< 0\)vô nghiệm
KL : vô nghiệm
Bài 2 :
a, \(\left(3x-1\right)\left(2x+7\right)-\left(x+1\right)\left(6x-5\right)-\left(18x-12\right)\)
\(=6x^2+21x-2x-7-6x^2+5x-6x+5-18x+12=10\)
Vậy biểu thức ko phụ thuộc vào biến
b, \(\left(x-y\right)\left(x^3+x^2y+xy^2+y^3\right)-x^4y^4\)
\(=x^4+x^3y+x^2y^2+xy^3-yx^3-y^2x^2-y^3x-y^4-x^4y^4\)
\(=x^4-y^4-x^4y^4\)Vậy biểu thức phụ thuộc vào biến

bài 1:
a. \((x+1)(x+3) - x(x+2)=7 \)
\(x^2+ 3x +x +3 - x^2 -2x =7\)
\(x^2+4x+3-x^2-2x=7\)
\(=> 2x+3=7\)
\(2x=4\)
\(x = 2\)
Bài 2:
a)
\((3x-5)(2x+11) -(2x+3)(3x+7) \)
\(= 6x^2 +33x-10x-55-6x^2-14x-9x-10\)
\(= (6x^2-6x^2)+(33x-10x-14x-9x)-(55+10)\)
\(=-65\)
\(\)
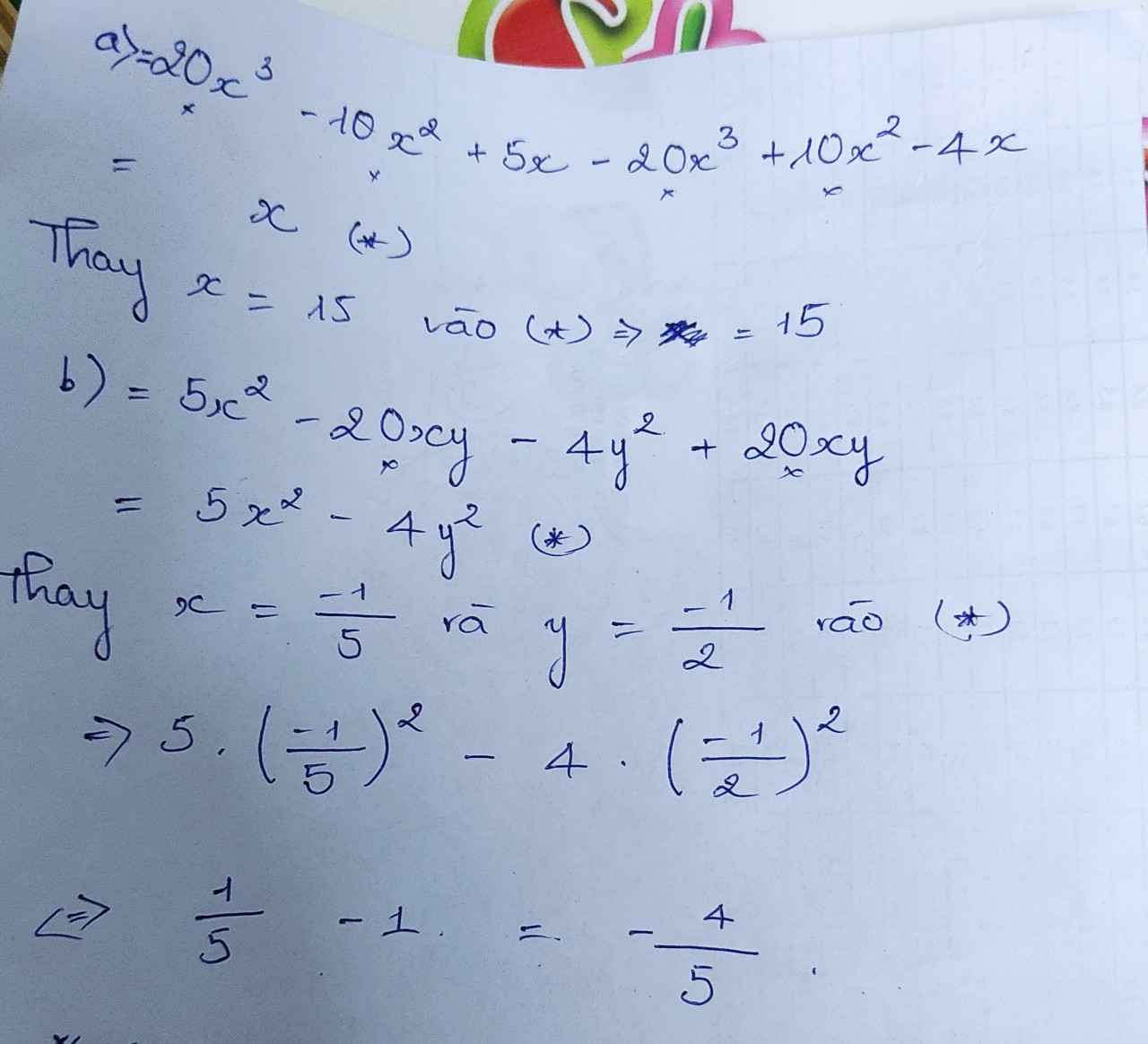

a) \(A=5x\left(4x^2-2x+1\right)-2x\left(10x^2-5x-2\right)\)
\(A=20x^3-10x^2+5x-20x^3+10x^2+4x\)
\(A=9x\)
Thay x = 15 vào, ta có:
\(A=9.15=135\)
b) \(B=5x\left(x-4y\right)-4y\left(y-5x\right)\)
\(B=5x^2-20xy-4y^2+20xy\)
\(B=5x^2-4y\)
Thay \(x=-\frac{1}{5};y=-\frac{1}{2}\) vào, ta có:
\(B=5.\left(-\frac{1}{5}\right)^2-4.\left(-\frac{1}{2}\right)=\frac{11}{5}\)
c) \(C=6xy\left(xy-y^2\right)-8x^2\left(x-y^2\right)-5y^2\left(x^2-xy\right)\)
\(C=6x^2y^2-6xy^3-8x^3+8x^2y^2-5x^2y^2+5xy^3\)
\(C=9x^2y^2-xy^3-8x^3\)
Thay \(x=\frac{1}{2};y=2\) vào, ta có:
\(C=9.\left(\frac{1}{2}\right)^2.2^2-\frac{1}{2}.2^3-8.\left(\frac{1}{2}\right)^3=4\)
d) \(D=\left(3x+5\right)\left(2x-1\right)+\left(4x-1\right)\left(3x+2\right)\)
\(D=6x^2-3x+10x-5+12x^2+8x-3x-2\)
\(D=18x^2+12x-7\)
Ta có: \(\left|2\right|=\orbr{\begin{cases}x=-2\\x=2\end{cases}}\)
+) Với x = -2
\(D=18.\left(-2\right)^2+12.\left(-2\right)-7=41\)
+) Với x = 2
\(D=18.2^2+12.2-7=89\)