Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đoạn thẳng f: Đoạn thẳng [B, C] Đoạn thẳng h: Đoạn thẳng [B, A] Đoạn thẳng j: Đoạn thẳng [A, D] Đoạn thẳng k: Đoạn thẳng [C, D] Đoạn thẳng l: Đoạn thẳng [E, A] Đoạn thẳng m: Đoạn thẳng [F, C] Đoạn thẳng n: Đoạn thẳng [C, A] Đoạn thẳng p: Đoạn thẳng [B, E] Đoạn thẳng q: Đoạn thẳng [B, F] Đoạn thẳng r: Đoạn thẳng [B, D] B = (-2.33, 0.59) B = (-2.33, 0.59) B = (-2.33, 0.59) C = (3.76, 0.04) C = (3.76, 0.04) C = (3.76, 0.04) Điểm A: Điểm trên g Điểm A: Điểm trên g Điểm A: Điểm trên g Điểm D: Giao điểm đường của g, i Điểm D: Giao điểm đường của g, i Điểm D: Giao điểm đường của g, i Điểm E: D đối xứng qua A Điểm E: D đối xứng qua A Điểm E: D đối xứng qua A Điểm F: D đối xứng qua C Điểm F: D đối xứng qua C Điểm F: D đối xứng qua C
a) Do E đối xứng với D qua A nên AD = AE.
Do ABCD là hình bình hành nên AD = BC; AD //BC.
Xét tứ giác AEBC có AE//BC; AE = BC nên nó là hình bình hành (dấu hiệu nhận biết)
b)
Do F đối xứng với D qua C nên DC = CF.
Do ABCD là hình bình hành nên AB = DC; AB // DC.
Xét tứ giác ABFC có AB//CF; AB = CF nên nó là hình bình hành (dấu hiệu nhận biết)
Do ABFC là hình bình hành nên AC // BF.
Do AEBC là hình bình hành nên AC // BE.
Theo tiên đề Oclit suy ra E, B, F thẳng hàng.
Do ABFC là hình bình hành nên \(\widehat{BAC}=\widehat{BFD}\) (Hai góc đối)
Hay \(\widehat{BAC}=\widehat{EFD}\)
c) Ta đã có E, B, F thẳng hàng.
Lại có EB = AC; BF = AC nên EB = BF.
Vậy E và F đối xứng nhau qua B.
d) Để E và F đối xứng nhau qua đường thẳng BD thì \(BD\perp EF\)
Lại có EF // AC nên \(BD\perp AC\)
Hình bình hành ABCD có hai đường chéo vuông góc thì nó trở thành hình thoi.
Vậy hình bình hành ABCD trở thành hình thoi thì E và F đối xứng nhau qua BD.

Bài 1 :
a. AB//CD (ABCD là hình bình hành) M thuộc AB N thuộc CD => BM // DN
Xét tứ giác AMCN có:
MB=DN (gt)
BM// DN
=> tứ giác AMCN là hình bình hành
b. Gọi giao điểm của AC và BD là O
=> O là trung điểm của AC và BD (tính chất hình bình hành)
Hình bình hành MBND có
O là trung điểm của BD
MN là đường chéo hình bình hành MBND
O là trung điểm MM
=> MN đi qua O
=> AC,BD,MN đồng quy tại một điểm
c.
Bài 2 :
a. AB = CD (ABCD là hình bình hành)
Mà AB = BE (A đối xứng E qua B)
=> CD=BE
AB // CD (ABCD là hình bình hành)
Mà E thuộc AC
=> CD//BE
Xét tứ giác DBEC:
CD=BE (CM)
CD//BE (CM)
=> DBEC là hình bình hành
b.

Giải :
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B

Bài giải:
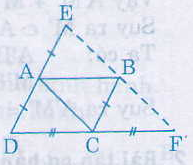
AE // BC (vì AD // BC)
AE = BC (cùng bằng AD)
nên ACBE là hình bình hành.
Suy ra: BE // AC, BE = AC (1)
Tương tự BF // AC, BF = AC (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF. Nên B là trung điểm của EF, vậy E đối xứng với F qua B.
❓