Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Không gian mẫu: \(C_{10}^3\)
Số cách chọn 3 số nguyên liên tiếp: 8 cách (123; 234;...;8910)
Số cách chọn ra 3 số trong đó có đúng 2 số nguyên liên tiếp:
- Cặp liên tiếp là 12 hoặc 910 (2 cách): số còn lại có 7 cách chọn
- Cặp liên tiếp là 1 trong 7 cặp còn lại: số còn lại có 6 cách chọn
Vậy có: \(C_{10}^3-\left(8+2.7+7.6\right)=56\) bộ thỏa mãn
Xác suất: \(P=\dfrac{56}{C_{10}^3}=...\)
b.
Có 2 số chia hết cho 4 là 4 và 8
Rút ra k thẻ: \(C_{10}^k\) cách
Số cách để trong k thẻ có ít nhất 1 thẻ chia hết cho 4: \(C_{10}^k-C_8^k\)
Xác suất thỏa mãn: \(P=\dfrac{C_{10}^k-C_8^k}{C_{10}^k}>\dfrac{13}{15}\)
\(\Leftrightarrow\dfrac{2}{15}>\dfrac{C_8^k}{C_{10}^k}=\dfrac{\dfrac{8!}{k!\left(8-k\right)!}}{\dfrac{10!}{k!\left(10-k\right)!}}=\dfrac{\left(9-k\right)\left(10-k\right)}{90}\)
\(\Leftrightarrow\left(9-k\right)\left(10-k\right)-12< 0\Leftrightarrow k^2-19k+78< 0\)
\(\Rightarrow6< k< 13\)

Đáp án D.
Nhận xét:
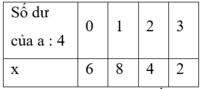
x chia hết cho 4 khi a chia 4 dư 1 hoặc dư 2. Dãy các số chia 4 dư 1 là: 1; 5; 9; …; 97 (có 25 số); dãy các số chia 4 dư 2 là 2; 6; 10; …; 98 (có 25 số).
Xác suất cần tím là: 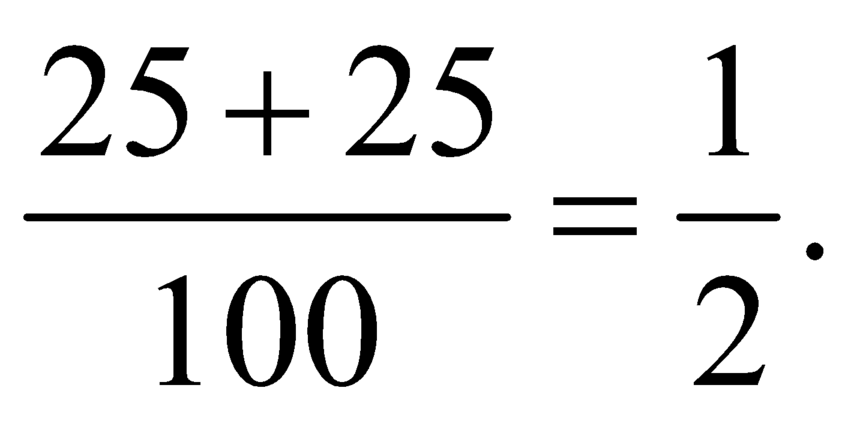

Chọn C
Ta có ![]()
Gọi số tự nhiên cần tìm có bốn chữ số là a b c d ¯
Vì a b c d ¯ chia hết cho 11 nên (a + c) - (b + d) ⋮ 11
=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do
![]()
![]()
Theo đề bài ta cũng có a + b + c + d chia hết cho 11
Mà ![]()
![]()
![]()
![]() hoặc
hoặc ![]()
Vì ![]()
![]() nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ
nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ

![]()
(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số:
![]()
- Chọn 2 cặp trong số 4 cặp trên ta có C 4 2 cách.
- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn d.
![]()
Vậy xác suất cần tìm là 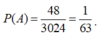

Chọn A
Giả sử số cần lập là ![]()
Số phần từ không gian mẫu: ![]()
Gọi A là biến cố lấy được số chia hết cho 11 và tổng của các chữ số của chúng cũng chia hết cho 11.
Ta có:
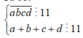
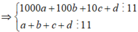
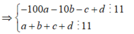
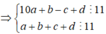
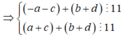
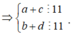
Từ 1,2,3,4,5,6,7,8,9 ta có 4 cặp tổng chia hết cho 11 là: ![]()

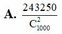
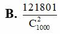
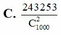
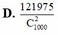

Câu 1: dài quá, làm biếng, bài này rất nổi tiếng, tìm là thấy liền :D
Câu 2:
Gọi 2 số đó là \(x< y\), số cách chọn ra 2 số là \(C_{2019}^2\)
Theo bài ra ta có: \(\left\{{}\begin{matrix}x^2+3y=a^2\\y^2+3x=b^2\end{matrix}\right.\)
Do \(x< y\Rightarrow x^2< x^2+3y< x^2+3x< \left(x+2\right)^2\)
\(\Rightarrow x^2+3y=\left(x+1\right)^2\Rightarrow3y=2x+1\Rightarrow x=\frac{3y-1}{2}\)
\(\Rightarrow y^2+3\left(\frac{3y-1}{2}\right)=b^2\Leftrightarrow2y^2+9y-3=2b^2\)
\(\Leftrightarrow\left(4y+9\right)^2-105=16b^2\)
\(\Leftrightarrow\left(4y-4b+9\right)\left(4y+3b+9\right)=105\)
Phương trình nghiệm nguyên này cho ta 2 nghiệm là \(y=1\Rightarrow x=1\left(l\right)\) và \(y=11\Rightarrow x=16\)
Vậy có đúng 1 cặp số tự nhiên thỏa mãn yêu cầu đề bài
\(\Rightarrow\) Xác suất \(P=\frac{1}{C_{2019}^2}\)
Sao nhỏ vậy ta?
Câu 3:
Không gian mẫu: \(9.A_9^7\)
Ta thấy tổng 10 chữ số phân biệt từ 0 đến 9 bằng 45
Do đó, tổng 8 chữ số phân biệt tối đa bằng \(45-1-0=44\), tối thiểu bằng \(45-9-8=28\)
Mà để tổng 8 số chia hết cho 45 \(\Rightarrow\) chia hết cho 9
\(\Rightarrow\) Tổng 8 chữ số phải bằng 36
Để ý 1 điều nữa là \(45-36=9\), do đó, để 8 chữ số có tổng 36 thì ta chỉ cần loại đi 1 cặp số có tổng là 9 từ 10 chữ số 0-9
- Nếu cặp bị loại là (0;9): số cuối có 1 cách chọn (5), 7 vị trí còn lại có \(7!\) cách hoán vị
- Cặp bị loại là (4;5): số cuối có 1 cách chọn (0), 7 vị trí còn lại có \(7!\) cách hoán vị
- Cặp bị loại ko chứa 0 hoặc 5 (gồm 18; 27; 36): nếu số cuối là 0 thì 7 vị trí còn lại có 7! cách hoán vị, nếu số cuối là 5 thì vị trí đầu có 6 cách chọn, 6 vị trí còn lại có 6! cách hoán vị \(\Rightarrow3.\left(7!+6.6!\right)\)
Vậy tổng cộng có: \(7!+7!+3\left(7!+6.6!\right)\) số
Xác suất: \(P=\frac{5.7!+18.6!}{9.A_9^7}=\frac{53}{2268}\)
Cách làm kiểu vậy, bạn coi lại mấy bước tính