Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Nhận xét:
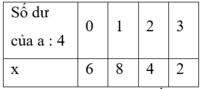
x chia hết cho 4 khi a chia 4 dư 1 hoặc dư 2. Dãy các số chia 4 dư 1 là: 1; 5; 9; …; 97 (có 25 số); dãy các số chia 4 dư 2 là 2; 6; 10; …; 98 (có 25 số).
Xác suất cần tím là: 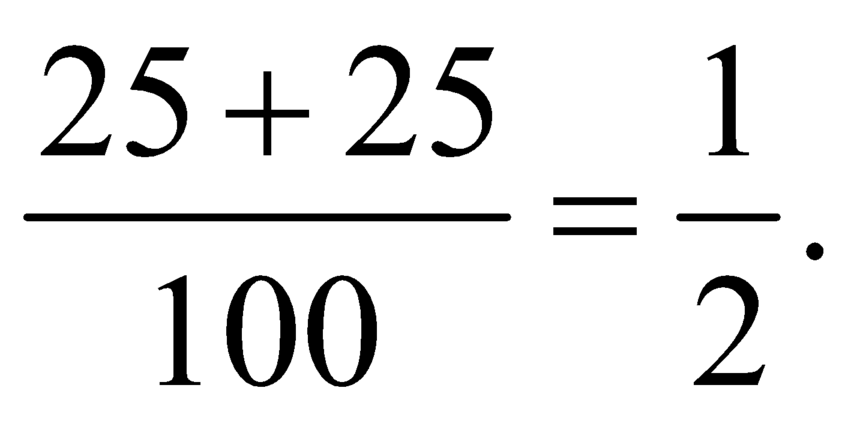

a. Không gian mẫu: \(C_{10}^3\)
Số cách chọn 3 số nguyên liên tiếp: 8 cách (123; 234;...;8910)
Số cách chọn ra 3 số trong đó có đúng 2 số nguyên liên tiếp:
- Cặp liên tiếp là 12 hoặc 910 (2 cách): số còn lại có 7 cách chọn
- Cặp liên tiếp là 1 trong 7 cặp còn lại: số còn lại có 6 cách chọn
Vậy có: \(C_{10}^3-\left(8+2.7+7.6\right)=56\) bộ thỏa mãn
Xác suất: \(P=\dfrac{56}{C_{10}^3}=...\)
b.
Có 2 số chia hết cho 4 là 4 và 8
Rút ra k thẻ: \(C_{10}^k\) cách
Số cách để trong k thẻ có ít nhất 1 thẻ chia hết cho 4: \(C_{10}^k-C_8^k\)
Xác suất thỏa mãn: \(P=\dfrac{C_{10}^k-C_8^k}{C_{10}^k}>\dfrac{13}{15}\)
\(\Leftrightarrow\dfrac{2}{15}>\dfrac{C_8^k}{C_{10}^k}=\dfrac{\dfrac{8!}{k!\left(8-k\right)!}}{\dfrac{10!}{k!\left(10-k\right)!}}=\dfrac{\left(9-k\right)\left(10-k\right)}{90}\)
\(\Leftrightarrow\left(9-k\right)\left(10-k\right)-12< 0\Leftrightarrow k^2-19k+78< 0\)
\(\Rightarrow6< k< 13\)

gọi\(\Omega\) là không gian mẫu để rút ra 10 tấm thẻ trong 30 tấm==>n(\(\Omega\))=C1030 =30045015
gọi A là biến cố "lấy 10 tấm thẻ trong đó có 5 tấm mang số lẻ, 5 tấm chẵn trong đó có 1 tấm chia hết cho 10"
nx: có 30 tấm đánh số từ 1->30 ------->15 tấm lẻ, 15 tấm chẵn, có 3 tấm chứa số 10, 20,30 là chia hết cho 10
- trường hợp rút 5 tấm lẻ là :C515 =3003 cách
- TH rút 5 tấm chẵn trong đó có 1 tấm chia hết cho 10 là
3xC412 =1485 cách
=======> n(A)=1485x3003=4459455 cách====>P(A)=99/667

Đáp án C
Chọn ra 8 tấm thẻ 1 cách ngẫu nhiên có ![]() cách
cách
Trong 20 tấm thẻ có 10 tấm mang số lẻ, có 5 tấm mang số chẵn không chia hết cho 4 và 5 tấm thẻ mang số chẵn chia hết cho 4
TH1: Lấy được 5 tấm mang số lẻ, 2 tấm mang số chẵn chia hết cho 4 và tấm mang 1 số chẵn không chi hết cho 4 có: ![]()
TH2: Lấy được 5 tấm mang số lẻ, 3 tấm mang số chẵn chia hết cho 4 có ![]() cách.
cách.
Vậy xác suất cần tìm là
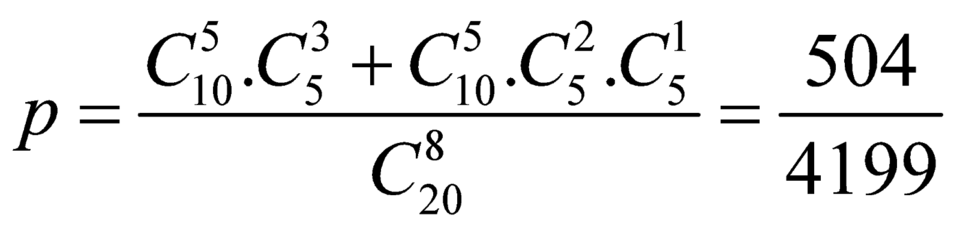

Haizz. Mik cx tham khảo rồi. Cái quan trọng là chọn chia hết cho 3