Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sắp xếp các gốc theo thứ tự từ lớn đến bé:
Ta có: \(AC>BC>AB\)
\(\Rightarrow\widehat{B}>\widehat{A}>\widehat{C}\)

a, Ta có góc đối diện với cạnh nhỏ nhất là góc lớn nhất
mà \(AB< AC< BC\left(4< 6< 7\right)\)
\(\Rightarrow\widehat{C}< \widehat{B}< \widehat{A}\)
Sắp xếp : \(\widehat{C},\widehat{B},\widehat{A}\)
b, Cách vẽ đường trung trực
Bước 1 Xác định trung điểm của MN
Giả sử : I là trung điểm MN
Bước 2 Vẽ \(IM=\dfrac{1}{2}MN=\dfrac{1}{2}.5=2,5\left(cm\right)\)
Bước 3 vẽ đường thẳng vuông góc với MN đi qua I
Hình vẽ :
M I N

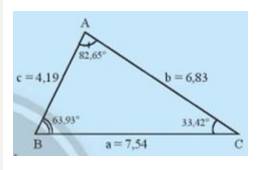
- Độ dài các cạnh từ nhỏ đến lớn là c, b, a
- Các góc từ nhỏ đến lớn là C, B, A
- Ta thấy trong tam giác ABC cạnh đối diện với góc lớn hơn thì lớn hơn và ngược lại.

xét tam giác ABM và tam giac AMD có
AB = AD ( gt)
AM chung
BM = MD ( M là trung điểm BD )
suy ra 2 tam giác bằng nhau

Câu 4: Cho tam giác ABC vuông tại A có AB = 8cm, AC = 6cm.
a, Tính độ dài cạnh BC của tam giác ABC.
b, Trên tia đối của ria AB lấy điểm D sao cho AD = AB, đường trung tuyến BK của tam giác BCD cắt AC tại E. Tính độ dài các đoạn thẳng EC và EA.
c, Chứng minh CB = CD.
* Hình tự vẽ
a)
Áp dụng định lý Pytago ta tính được cạnh huyền BC = 10cm
b)
Xét tam giác DBC, ta có:
BK là trung tuyến ứng với cạnh CD ( gt )
CA là trung tuyến ứng với cạnh BD ( AB = AD )
BK giao với CA tại E
=> E là trọng tâm của tam giác BDC
=> CE = \(\frac{2AC}{3}\)= 4cm ; AE = 2cm
c)
Xét tam giác BDC, ta có:
CA là trung tuyến ứng với cạnh BD
CA là đường cao ứng với cạnh BD
=> Tam giác BDC cân tại C
=> CB = CD
Câu 5: Cho tam giác ABC có góc A = 50 độ, góc B = 60 độ, góc C = 70 độ. Hãy so sánh các cạnh của tam giác ABC
B A C
Theo đề ra: Góc A = 50 độ
Góc B = 60 độ
Góc C = 70 độ
=> Góc A < góc B < góc C
=> BC < AC < AB ( quan hệ giữa góc và cạnh đối diện trong một tam giác )

chả hiểu chi cả???????????????????????????????????????????????????????????????????????????????????????????????????
a: góc B<góc A<góc C
=>AC<BC<AB
b: