K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
19 tháng 6 2017
Lời giải của bạn Hà sai, lời giải của bạn Quang đúng.
Vì 5x4 chia hết cho 2x2;
–4x3 chia hết cho 2x2;
6x2y chia hết cho 2x2
Do đó A = 5x4 – 4x3 + 6x2y chia hết cho 2x2 hay A chia hết cho B.
Chú ý: Đơn thức A chia hết cho đơn thức B nếu tìm được đơn thức Q sao cho A=B.Q
Ví dụ : Cho hai đơn thức A= 2x2y3; B = 7xy
Khi đó với đơn thức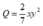 
thì A=B.Q
Do đó, đơn thức A chia hết cho đơn thức B.
29 tháng 10 2023
a: \(\left(n+3\right)^2-n^2=\left(n+3+n\right)\left(n+3-n\right)\)
\(=3\left(2n+3\right)⋮3\)
b: Đặt A=\(\left(n-5\right)^2-n^2\)
\(A=\left(n-5\right)^2-n^2\)
\(=n^2-10n+25-n^2\)
\(=-10n+25=5\left(-2n+5\right)⋮5\)
\(A=\left(n-5\right)^2-n^2\)
\(=-10n+25\)
\(-10n⋮2;25⋮̸2\)
=>-10n+25 không chia hết cho 2
=>A không chia hết cho 2
KV
29 tháng 10 2023
(n + 3)² - n² = n² + 6n + 9 - n²
= 6n + 9
= 3(3n + 3) ⋮ 3
Vậy [(n + 3)² - n²] ⋮ 3 với mọi n ∈ ℕ
--------
(n - 5)² - n² = n² - 10n + 25 - n²
= -10n + 25
= -5(2n - 5) ⋮ 5
Do -10n ⋮ 2
25 không chia hết cho 2
⇒ -10n + 25 không chia hết cho 2
Vậy [(n - 5)² - n²] ⋮ 5 và không chia hết cho 2 với mọi n ∈ ℕ
22 tháng 10 2023
Tập hợp các số có 2 chữ số chia hết cho cả 3 và 5 là:
A={15;30;45;60;75;90}
=>n(A)=6
Tập hợp các số có 2 chữ số chia hết cho 3 là:
B={12;15;...;99}
=>\(n\left(B\right)=\dfrac{99-12}{3}+1=30\)
Tập hợp các số có 2 chữ số chia hết cho 5 là:
C={10;15;20;...;95}
=>\(n\left(C\right)=\dfrac{95-10}{5}+1=\dfrac{85}{5}+1=18\left(số\right)\)
Số số có 2 chữ số chia hết cho 3 hoặc 5 và không đồng thời chia hết cho 3 và 5 là:
\(n\left(B\right)+n\left(C\right)-n\left(A\right)=30+18-6=42\)
AH
Akai Haruma
Giáo viên
9 tháng 8 2021
Lời giải:
$A=p^4+2019q^4=p^4-q^4+2020q^4$
$=(p^2-q^2)(p^2+q^2)+2020q^4$
Vì $p,q$ là số nguyên tố lớn hơn 5 nên $(p,5)=(q,5)=1$
$\Rightarrow p^2,q^2\equiv 1,4\pmod 5$
Nếu $p^2\equiv q^2\pmod 5$ thì $p^2-q^2\equiv 0\pmod 5$
$\Rightarrow A=(p^2-q^2)+2020q^4\equiv 0 \pmod 5(1)$
Nếu $p^2,q^2$ không cùng số dư khi chia cho $5$ thì:
$p^2+q^2\equiv 1+4\equiv 0\pmod 5$
$\Rightarrow A\equiv 0\pmod 5(2)$
Từ $(1);(2)\Rightarrow A\vdots 5(*)$
Mặt khác:
Vì $p,q>5$ nên $p,q$ lẻ
$\Rightarrow p^2\equiv q^2\equiv 1\pmod 4$
$\Rightarrow p^2-q^2\equiv 0\pmod 4$
$\Rightarrow A=(p^2-q^2)(p^2+q^2)+2020q^4\equiv 0\pmod 4$
$\Rightarrow A\vdots 4(**)$
Từ $(*); (**)\Rightarrow A\vdots (4.5=20)$
20 tháng 4 2017
Bài giải:
Ta có: A : B = (5x4 – 4x3 + 6x2y) : 2x2
= (5x2 : 2x2) + (– 4x3 : 2x2) + (6x2y : 2x2)
= x2 – 2x + 3y
Như vậy A chia hết cho B vì mọi hạng tử của A đều chia hết cho B.
Vậy: Quang trả lời đùng, Hà trả lời sai.
LT
20 tháng 4 2017
Ta có: A : B = (5x4 – 4x3 + 6x2y) : 2x2
= (5x2 : 2x2) + (– 4x3 : 2x2) + (6x2y : 2x2)
= 5252x2 – 2x + 3y
Như vậy A chia hết cho B vì mọi hạng tử của A đều chia hết cho B.
Vậy: Quang trả lời đùng, Hà trả lời sai.
25 tháng 12 2019
Từ 1 đến 100 có số số chia hết cho 2 là:
(100-2):2+1=50(số)
Từ 1 đến 100 có số số chia hết cho 2 và 3 là:
(96-6):6+1=16(số)
=>Từ 1 đến 100 có số số chia hết cho 2 mà không chia hết cho 3 là:
50-16=34(số)
25 tháng 12 2019
Từ 1 đến 1000 có số số chia hết cho 2 là :
(1000-2):2+1=500 ( số )
Từ 1 đến 1000 có số số chia hết cho 2 mà không chia hết cho 3 là :
(996 - 6 ) : 6 + 1 = 166 ( số )
Vậy có 166 số chia hết cho 2 mà không chia hết cho 3
không chia hết \(\pi⋮̸2\) \(\pi=3,14\)