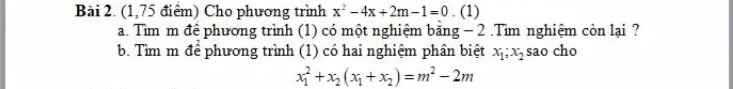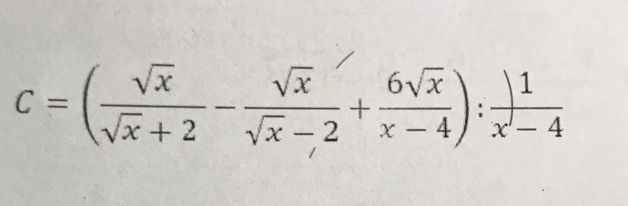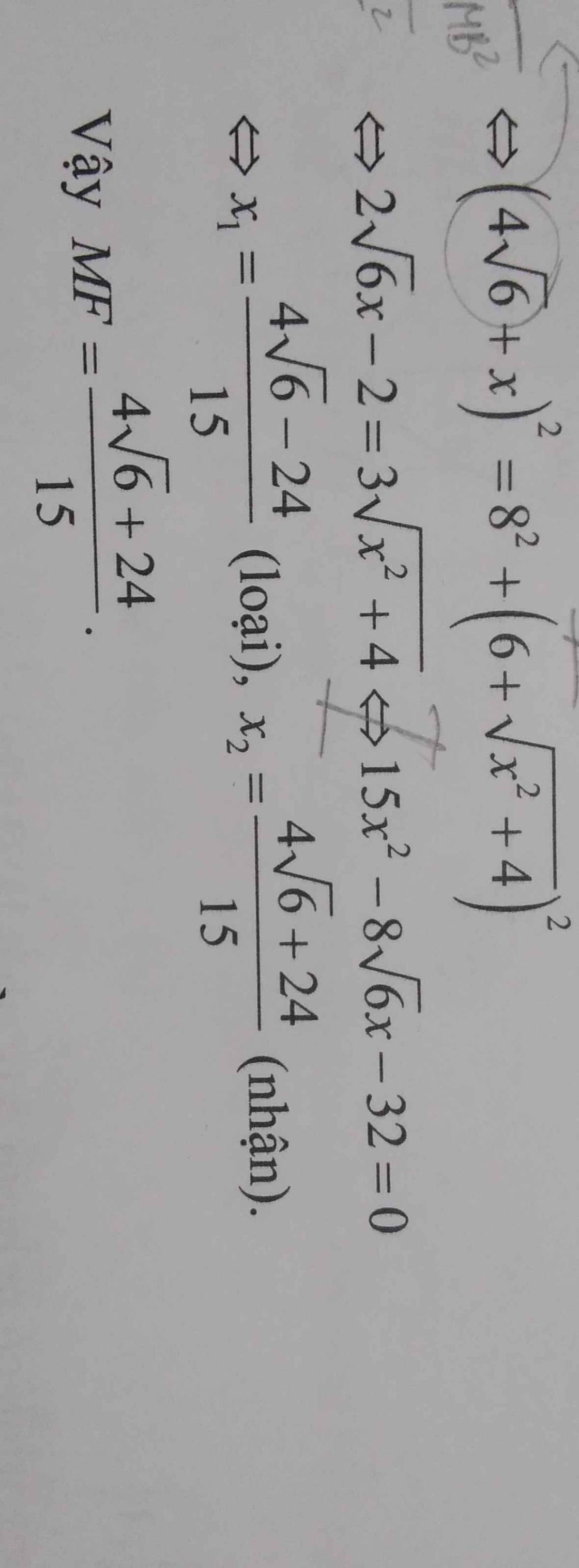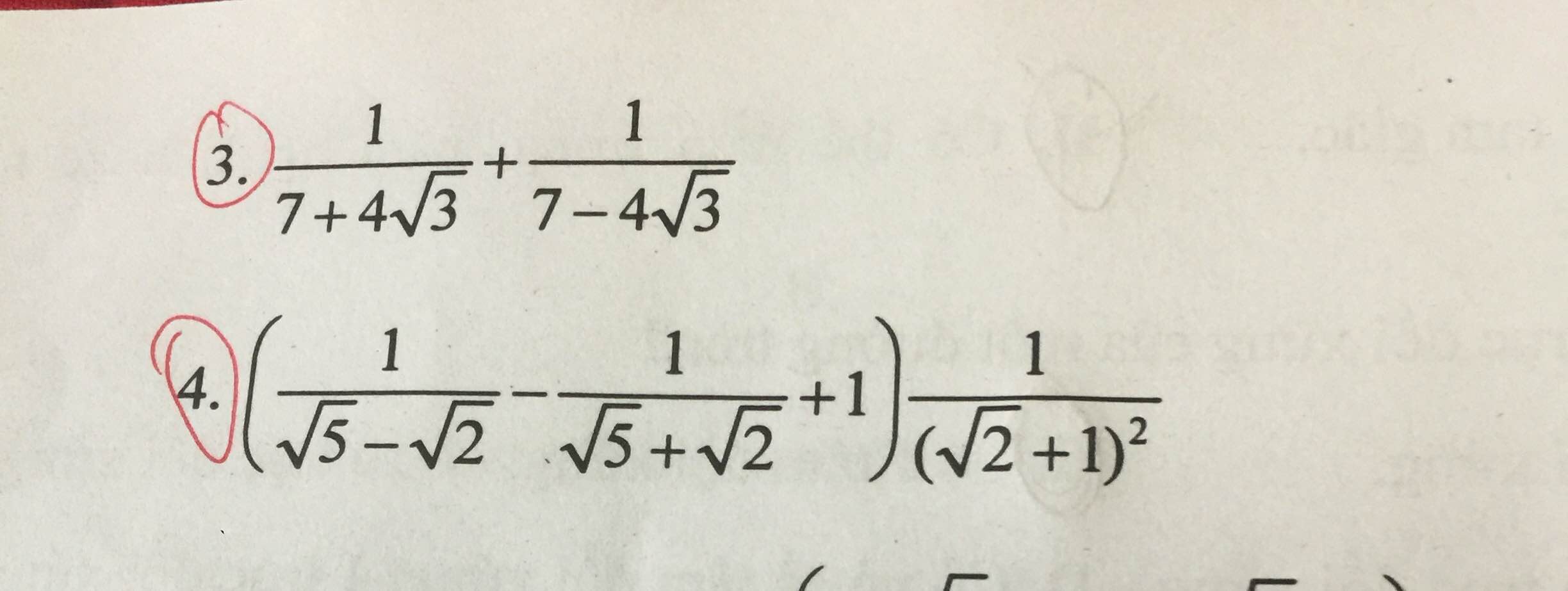Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Thay x=-2 vào (1), ta được:
4+8+2m-1=0
=>2m+11=0
hay m=-11/2
b: \(\text{Δ}=\left(-4\right)^2-4\left(2m-1\right)\)
=16-8m+4
=-8m+20
Để phương trình có hai nghiệm phân biệt thì -8m+20>0
=>-8m>-20
hay m<5/2
Theo đề, ta có: \(x_1^2+x_2^2+x_1x_2=m^2-2m\)
\(\Leftrightarrow m^2-2m=\left(x_1+x_2\right)^2-x_1x_2\)
\(\Leftrightarrow m^2-2m=\left(-4\right)^2-\left(2m-1\right)\)
\(\Leftrightarrow m^2-2m=16-2m+1=17\)
hay \(m=-\sqrt{17}\)

\(C=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)-\sqrt{x}\left(\sqrt{x}+2\right)+6\sqrt{x}}{x-4}.\left(x-4\right)=2\sqrt{x}\)

a: Xét ΔSBM và ΔSNB có
\(\widehat{SBM}=\widehat{SNB}\)
\(\widehat{BSM}\) chung
Do đó: ΔSBM\(\sim\)ΔSNB
Suy ra: SB/SN=SM/SB
hay \(SB^2=SM\cdot SN\)
b: Xét (O) có
SA là tiếp tuyến
SB là tiếp tuyến
Do đó: SA=SB
mà OA=OB
nên SO là đường trung trực của AB
=>SO⊥AB
Xét ΔOBS vuông tại B có BH là đường cao
nên \(SH\cdot SO=SB^2=SM\cdot SN\)

5:
a: Xét ΔABC vuông tại A có
\(sinC=\dfrac{3}{5}\)
=>\(\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\dfrac{3}{BC}=\dfrac{3}{5}\)
=>BC=5(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16\)
=>AC=4(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\CH\cdot CB=CA^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\\CH=\dfrac{4^2}{5}=3,2\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(tanB=\dfrac{4}{3}\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
b: Xét ΔABF vuông tại A có AE là đường cao
nên \(BE\cdot BF=AB^2\left(1\right)\)
Xét ΔBAC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BE\cdot BF=BH\cdot BC\)
XétΔABC vuông tại A có AH là đường cao
nên \(CH\cdot CB=CA^2\)
\(\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot CB}=\dfrac{BH}{CH}\)
c: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB
=>\(\widehat{MAB}=\widehat{MBA}\)
Xét ΔEAB vuông tại E và ΔHBA vuông tại H có
AB chung
\(\widehat{EAB}=\widehat{HBA}\)
Do đó: ΔEAB=ΔHBA
=>\(\widehat{DAB}=\widehat{DBA}\)
=>DA=DB
\(\widehat{DAB}+\widehat{DAF}=90^0\)
\(\widehat{DBA}+\widehat{DFA}=90^0\)
mà \(\widehat{DAB}=\widehat{DBA}\)
nên \(\widehat{DAF}=\widehat{DFA}\)
=>DA=DF
=>DF=DB
=>D là trung điểm của FB

ĐKXĐ: x>=-3/2
\(2x-3\sqrt{2x+3}-7=0\)
=>\(2x+3-3\sqrt{2x+3}-10=0\)
=>\(2x+3-5\sqrt{2x+3}+2\sqrt{2x+3}-10=0\)
=>\(\sqrt{2x+3}\left(\sqrt{2x+3}-5\right)+2\left(\sqrt{2x+3}-5\right)=0\)
=>\(\left(\sqrt{2x+3}-5\right)\left(\sqrt{2x+3}+2\right)=0\)
=>\(\sqrt{2x+3}-5=0\)
=>\(\sqrt{2x+3}=5\)
=>2x+3=25
=>2x=22
=>\(x=\dfrac{22}{2}=11\)

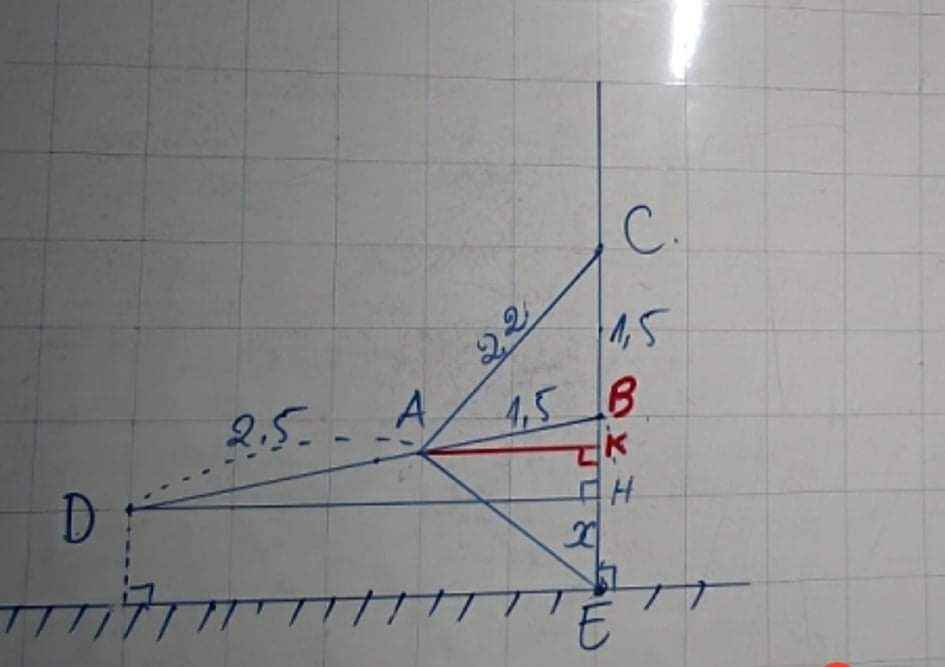
Gọi DH là khoảng cách thấp nhất từ máy bay đến mặt đất, khi đó AC có độ dài lớn nhất là 2,2m. Dựng hình chữ nhật DHEK => DH = EK
Do BA = BE = BC = 1,5m cố định nên tam giác ACE vuông tại A
Xét tam giác ACE vuông tại A có cos\(\widehat{ECA}\) = \(\dfrac{CA}{CE}=\dfrac{2,2}{3}\) => \(\widehat{ECA}\) \(\approx\) 42o50'
BA = BC => tam giác ABC cân tại B => \(\widehat{BAC}=\widehat{BCA}\) = \(\widehat{ECA}\) \(\approx\) 42o50'
=> \(\widehat{DBK}\) = \(\widehat{BAC}+\widehat{BCA}\) = 2.\(\widehat{BCA}\) = 85o40'
Xét tam giác DBK vuông tại D có: BK = BD. cos\(\widehat{DBK}\)
= 4.cos85o40' \(\approx\) 0,3022
=> DH = KE \(\approx\) 1,5 - 0,3022 \(\approx\)1,2 (m)


`(4\sqrt{6}+x)^2=8^2+(6+\sqrt{x^2+4})^2`
`<=>96+8\sqrt{6}x+x^2=64+36+12\sqrt{x^2+4}+x^2+4`
`<=>2\sqrt{6}x-2=3\sqrt{x^2+4}` `ĐK: x >= \sqrt{6}/6`
`<=>24x^2-8\sqrt{6}x+4=9x^2+36`
`<=>15x^2-8\sqrt{6}x-32=0`
`<=>x^2-[8\sqrt{6}]/15x-32/15=0`
`<=>(x-[4\sqrt{6}]/15)^2-64/25=0`
`<=>|x-[4\sqrt{6}]/15|=8/5`
`<=>[(x=[24+4\sqrt{6}]/15 (t//m)),(x=[-24+4\sqrt{6}]/15(ko t//m)):}`

3: \(=7-4\sqrt{3}+7+4\sqrt{3}=14\)
4: \(=\left(\dfrac{\sqrt{5}+\sqrt{2}-\sqrt{5}+\sqrt{2}+3}{3}\right)\cdot\dfrac{1}{3+2\sqrt{2}}=\dfrac{1}{3}\)