
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Hình 1:
Ta thấy $\widehat{xAB}=\widehat{ABy}=120^0$, mà 2 góc này ở vị trí so le trong nên $Ax\parallel By(1)$
Lại có:
$\widehat{ABy}+\widehat{yBC}+\widehat{ABC}=360^0$
$120^0+\widehat{yBC}+80^0=360^0$
$\widehat{yBC}=160^0$
Vậy: $\widehat{yBC}=\widehat{BCz}=160^0$. Mà hai góc này ở vị trí so le trong nên $By\parallel Cz(2)$
Từ $(1);(2)\Rightarrow Ax\parallel By\parallel Cz$
----------------------
Hình 2:
$\widehat{xAB}+\widehat{ABy}=65^0+115^0=180^0$, mà 2 góc này ở vị trí trong cùng phía nên $Ax\parallel By(1)$
$\widehat{CBy}+\widehat{BCz}=130^0+50^0=180^0$, mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Cz(2)$
Từ $(1);(2)\Rightarrow Ax\parallel By\parallel Cz$

\(\dfrac{x+y}{2+3}=\dfrac{24}{5}=4.8\)
X = 2 . 4.8=9.6/y =3 .4.8= 14.4
câu b làm i trang
bài 2 và câu c chừng nào cô mình dạy rồi mình lài tiếp cho
Không thì để mình đi tiềm hiểu một tí rồi mình làm cho
câu c
bài 2gọi chu vi của các cạnh lần lược là xyz (0 nhỏ hơn xyz nhỏ hơn 24)
Ta có x + y+z = 180
\(\dfrac{x+y+z}{2+4+5}=\dfrac{24}{11}\)
X = 2 . 24/11= 48/11
Y=4.24/11=96/11
Z= 5.24/11=120/11
Mình doán đại đó
Tại bài này cô mình chưa dạy







 giúp mình với ,ngày mai mình phải nộp rồi, cảm ơn
giúp mình với ,ngày mai mình phải nộp rồi, cảm ơn giúp mình với ngày mai mình phải nộp rồi, mình trân thành cảm ơn
giúp mình với ngày mai mình phải nộp rồi, mình trân thành cảm ơn
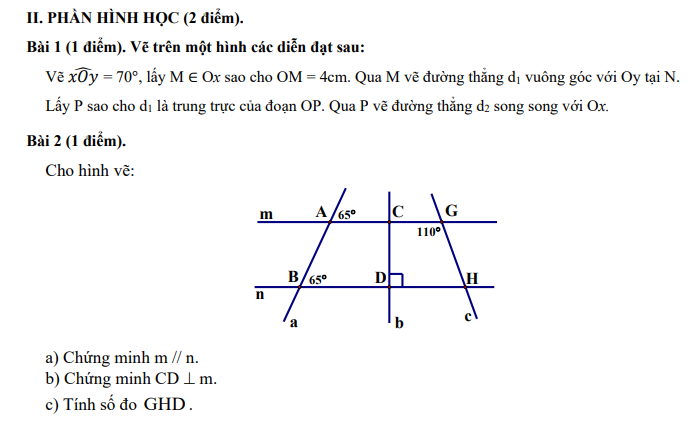



 Các bạn giúp mình làm mấy bài này ngày mai mình phải nộp rồi 😔
Các bạn giúp mình làm mấy bài này ngày mai mình phải nộp rồi 😔

\(c,\Leftrightarrow\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{6};2x+y=14\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{6}=\dfrac{2x+y}{4+3}=\dfrac{14}{7}=2\\ \Leftrightarrow\left\{{}\begin{matrix}x=4\\y=6\\z=12\end{matrix}\right.\)
\(d,\dfrac{x}{2}=\dfrac{y}{3}\Leftrightarrow\dfrac{x}{10}=\dfrac{y}{15};\dfrac{y}{5}=\dfrac{z}{7}\Leftrightarrow\dfrac{y}{15}=\dfrac{z}{21}\\ \Leftrightarrow\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{98}{46}=2\\ \Leftrightarrow\left\{{}\begin{matrix}x=20\\y=30\\z=42\end{matrix}\right.\)
Bài 2:
giải:gọi số hs của 3 tổ lần lượt là a,b,c(a,b,c >0)
Theo bài ra ,ta có:
a/2=b/3=c/4 và a+b+c=45
áp dụng tính chất dãy tỉ số bằng nhau:
a/2=b/3=c/4=a+b+c/2+3+4=45/9=5
Vậy a=5.2=10
b=5.3=15
c=5.4=20
Câu 3:
giải:gọi số hs thích các môn lần lượt là a,b,c(a,b,c >0)
Theo bài ra ta có:
a/2=b/3=c/5 và c-a=6
áp dụng tính chất dãy tỉ số bằng nhau ta có:
a/2=b/3=c/5=c-a/-2=6/3=2
Vậy a=2.2=4
b=2.3=6
c=2.5=10