Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

=>2x-2y=1 và 2x+2y=-1
=>4x=0 và x-y=1/2
=>x=0 và y=0-1/2=-1/2
Có cách bấm máy tính 570vn plus không ạ em cần biết cách bấm máy tính ạ

17.
\(f\left(x\right)>0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\left(luôn-đúng\right)\\\Delta'=\left(2m-1\right)^2-\left(3m^2-2m+4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow m^2-2m-3< 0\)
\(\Leftrightarrow-1< m< 3\)
\(\Rightarrow m=\left\{0;1;2\right\}\)
18.
\(\pi< x< \dfrac{3\pi}{2}\Rightarrow cosx< 0\)
\(\Rightarrow cosx=-\sqrt{1-sin^2x}=-\dfrac{\sqrt{5}}{3}\)
\(\Rightarrow tanx=\dfrac{sinx}{cosx}=\dfrac{2\sqrt{5}}{5}\)
\(tan\left(x+\dfrac{\pi}{4}\right)=\dfrac{tanx+tan\dfrac{\pi}{4}}{1-tanx.tan\dfrac{\pi}{4}}=\dfrac{\dfrac{2\sqrt{5}}{5}+1}{1-\dfrac{2\sqrt{5}}{5}.1}=9+4\sqrt{5}\)
19.
\(a^2=b^2+c^2+bc\Rightarrow b^2+c^2-a^2=-bc\)
\(\Rightarrow cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{-bc}{2bc}=-\dfrac{1}{2}\)
\(\Rightarrow A=120^0\)
20.
Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=2\)
\(d\left(I;\Delta\right)=\dfrac{\left|2-1-3\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
Gọi H là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}IH=d\left(I;\Delta\right)\\AH=\dfrac{1}{2}AB\end{matrix}\right.\)
Áp dụng định lý Pitago trong tam giác vuông IAH:
\(IA^2=IH^2+AH^2\Leftrightarrow R^2=IH^2+AH^2\)
\(\Rightarrow AH=\sqrt{2}\Rightarrow AB=2AH=2\sqrt{2}\)

Câu 10 sai, đáp án B đúng, sử dụng đan dấu trên trục số dễ dàng thấy:

12. Câu này sai, A mới đúng. Đơn giản là em nhìn kĩ lại công thức lượng giác là thấy thôi, nhầm lẫn về hệ số trong công thức biến tích thành tổng
\(cosa.cosb=\dfrac{1}{2}....\)
14. Đáp án C đúng
\(\overrightarrow{BA}=\left(2;2\right)=2\left(1;1\right)\) nên trung trực AB nhận (1;1) là 1 vtpt
Gọi M là trung điểm AB \(\Rightarrow M\left(0;2\right)\)
Phương trình: \(1\left(x-0\right)+1\left(y-2\right)=0\Leftrightarrow x+y-2=0\)

12 sai, C mới là đáp án đúng
13 sai, A đúng, \(sin-sin=2cos...sin...\)
18.
\(\Leftrightarrow\left\{{}\begin{matrix}a=m>0\\\Delta'=m^2-m\left(-m+3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\2m^2-3m< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>0\\0< m< \dfrac{3}{2}\end{matrix}\right.\) \(\Rightarrow m=1\)
Đáp án B
22.
Để pt có 2 nghiệm pb \(\Leftrightarrow\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(2m-3\right)^2-\left(m-2\right)\left(5m-6\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\-m^2+4m-3>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\1< m< 3\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2\left(2m-3\right)}{m-2}\\x_1x_2=\dfrac{5m-6}{m-2}\end{matrix}\right.\)
\(\dfrac{-2\left(2m-3\right)}{m-2}+\dfrac{5m-6}{m-2}\le0\)
\(\Leftrightarrow\dfrac{m}{m-2}\le0\) \(\Leftrightarrow0\le m< 2\)
Kết hợp điều kiện delta \(\Rightarrow1< m< 2\)
24.
Đề bài câu này dính lỗi, ko có điểm M nào cả, chắc là đường thẳng đi qua A
Đường tròn (C) tâm I(1;-2) bán kính R=4
\(\overrightarrow{IA}=\left(1;3\right)\)
Gọi d là đường thẳng qua A và cắt (C) tại 2 điểm B và C. Gọi H là trung điểm BC
\(\Rightarrow IH\perp BC\Rightarrow IH=d\left(I;d\right)\)
Theo định lý đường xiên - đường vuông góc ta luôn có: \(IH\le IA\)
Áp dụng Pitago cho tam giác vuông IBH:
\(BH=\sqrt{IB^2-IH^2}\Leftrightarrow\dfrac{BC}{2}=\sqrt{16-IH^2}\)
\(\Rightarrow BC_{min}\) khi \(IH_{max}\Leftrightarrow IH=IA\)
\(\Leftrightarrow IA\perp d\Rightarrow d\) nhận \(\overrightarrow{IA}\) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)+3\left(y-1\right)=0\Leftrightarrow x+3y-5=0\)

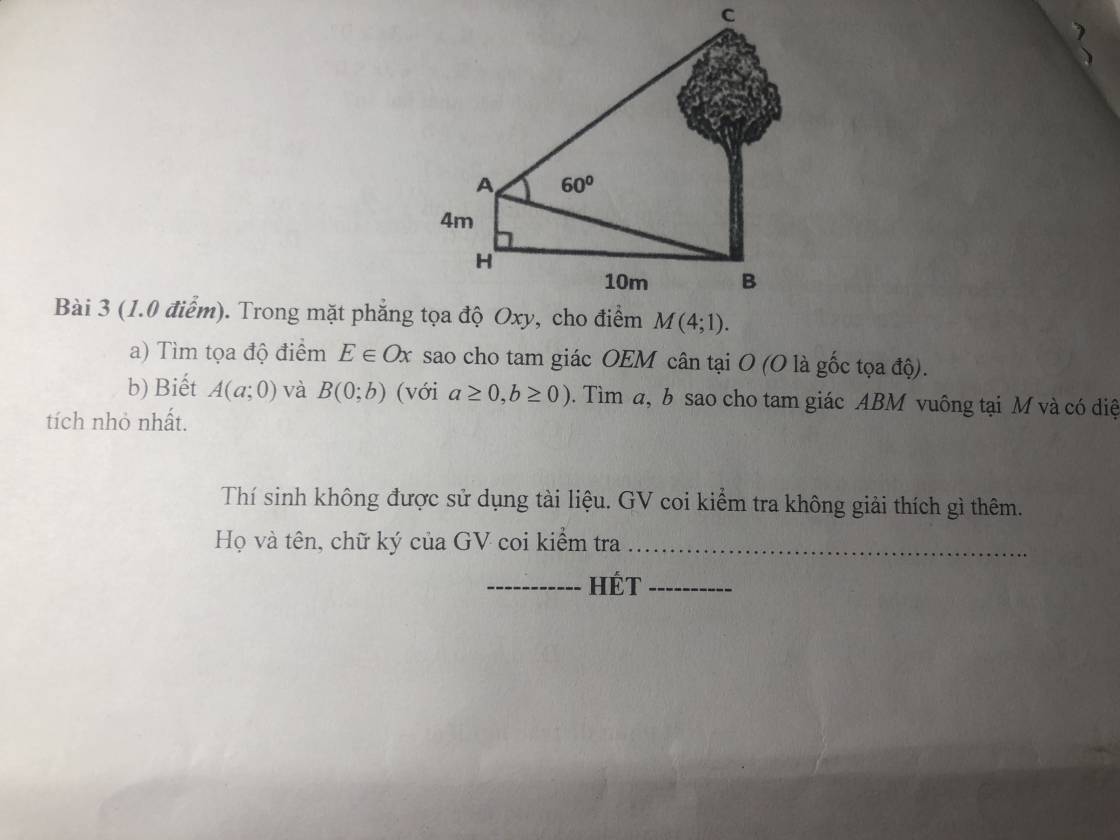
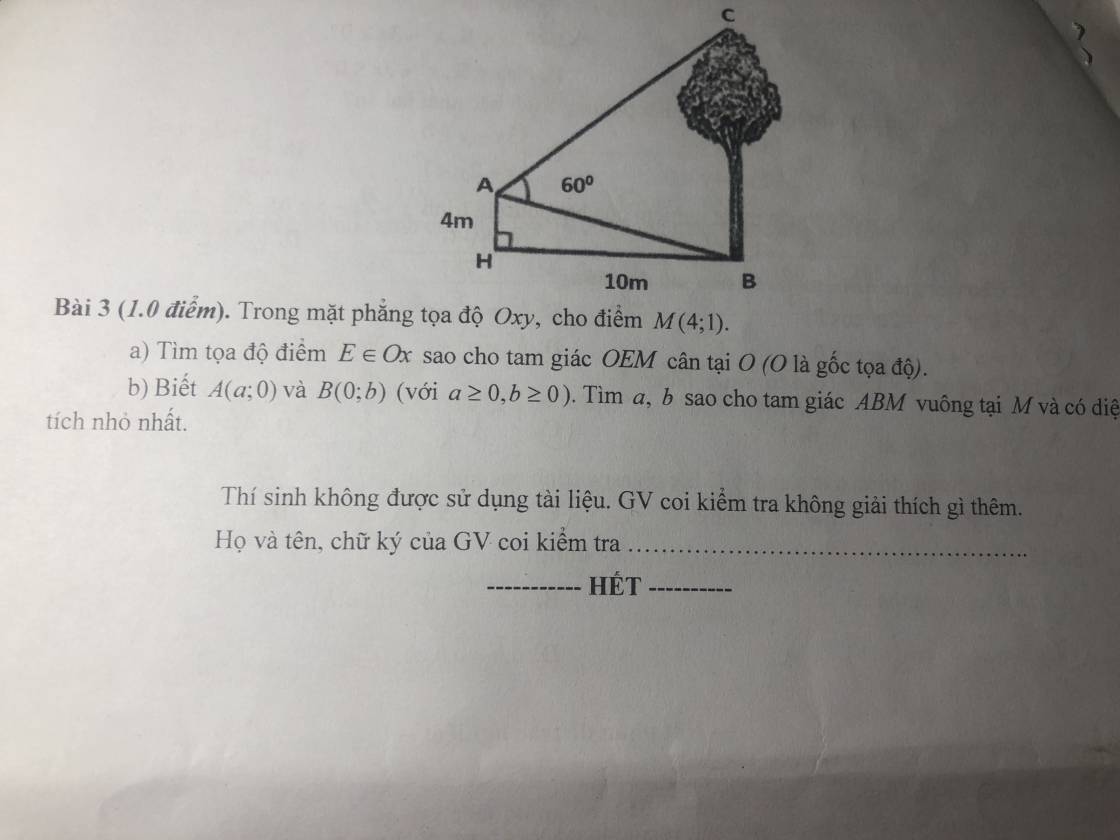
a: E thuộc Ox nên E(x;0)
O(0;0); M(4;1); E(x;0)
\(OM=\sqrt{\left(4-0\right)^2+\left(1-0\right)^2}=\sqrt{17}\)
\(OE=\sqrt{\left(x-0\right)^2+\left(0-0\right)^2}=\sqrt{x^2}=\left|x\right|\)
Để ΔOEM cân tại O thì OE=OM
=>\(\left|x\right|=\sqrt{17}\)
=>\(x=\pm\sqrt{17}\)

2.
Gọi \(H\left(x;y\right)\) là toạ độ chân đường cao ứng với BC \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(x-1;y+2\right)\\\overrightarrow{BC}=\left(2;1\right)\end{matrix}\right.\)
Do AH vuông góc BC \(\Rightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Rightarrow2\left(x-1\right)+y+2=0\Leftrightarrow y=-2x\)
\(\Rightarrow H\left(x;-2x\right)\Rightarrow\overrightarrow{BH}=\left(x+2;-2x-3\right)\)
Do H thuộc BC nên B, C, H thẳng hàng hay các vecto \(\overrightarrow{BC};\overrightarrow{BH}\) cùng phương
\(\Rightarrow\dfrac{x+2}{2}=\dfrac{-2x-3}{1}\Rightarrow x=\dfrac{8}{5}\Rightarrow y=-\dfrac{16}{5}\) \(\Rightarrow H\left(-\dfrac{8}{5};\dfrac{16}{5}\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(-\dfrac{13}{5};\dfrac{26}{5}\right)\Rightarrow\left\{{}\begin{matrix}AH=\sqrt{\left(-\dfrac{13}{5}\right)^2+\left(-\dfrac{6}{5}\right)^2}=\dfrac{13\sqrt{5}}{5}\\BC=\sqrt{2^2+1^2}=\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{13}{2}\)
3.
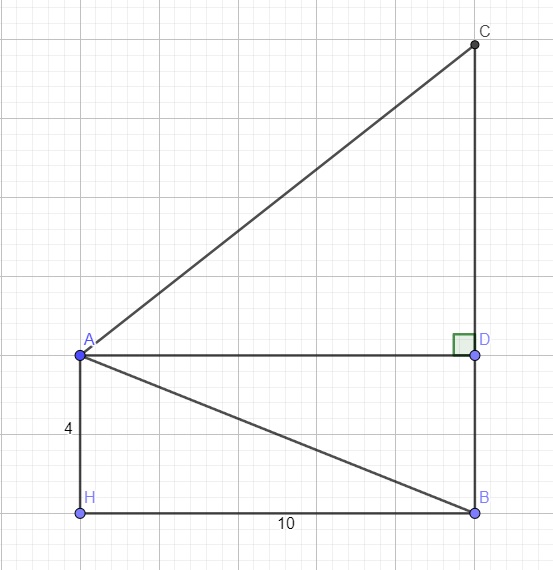
Kẻ AD vuông góc BC tại D
\(\Rightarrow AD=BH=10\) ; \(BD=AH=4\)
\(tan\widehat{BAD}=\dfrac{BD}{AD}=\dfrac{2}{5}\Rightarrow\widehat{BAD}\approx21^048'5''\)
\(\Rightarrow\widehat{CAD}=60^0-\widehat{BAD}=38^011'55''\)
\(\Rightarrow CD=AD.tan\widehat{CAD}=7,87\left(m\right)\)
\(\Rightarrow BC=BD+CD=11,87\left(m\right)\)

a.
D E thuộc Ox \(\Rightarrow\) tọa độ E có dạng \(E\left(x;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{OE}=\left(x;0\right)\\\overrightarrow{OM}=\left(4;1\right)\end{matrix}\right.\)
Tam giác OEM cân tại O \(\Rightarrow OE=OM\)
\(\Rightarrow\sqrt{x^2+0^2}=\sqrt{4^2+1^2}\Rightarrow x^2=17\)
\(\Rightarrow x=\pm\sqrt{17}\Rightarrow\left[{}\begin{matrix}E\left(\sqrt{17};0\right)\\E\left(-\sqrt{17};0\right)\end{matrix}\right.\)
b.
\(\left\{{}\begin{matrix}\overrightarrow{MA}=\left(a-4;-1\right)\\\overrightarrow{MB}=\left(-4;b-1\right)\end{matrix}\right.\)
Tam giác ABM vuông tại M \(\Rightarrow\overrightarrow{MA}.\overrightarrow{MB}=0\)
\(\Rightarrow-4\left(a-4\right)-1\left(b-1\right)=0\)
\(\Leftrightarrow4a+b-17=0\Rightarrow b=17-4a\)
Lại có \(S_{ABM}=\dfrac{1}{2}MA.MB=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{\left(b-1\right)^2+16}\)
\(=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{\left(16-4a\right)^2+16}=\dfrac{1}{2}\sqrt{\left(a-4\right)^2+1}.\sqrt{16\left[\left(a-4\right)^2+1\right]}\)
\(=2\left[\left(a-4\right)^2+1\right]\ge2\)
Dấu "=" xảy ra khi \(a-4=0\Rightarrow a=4\Rightarrow b=1\)

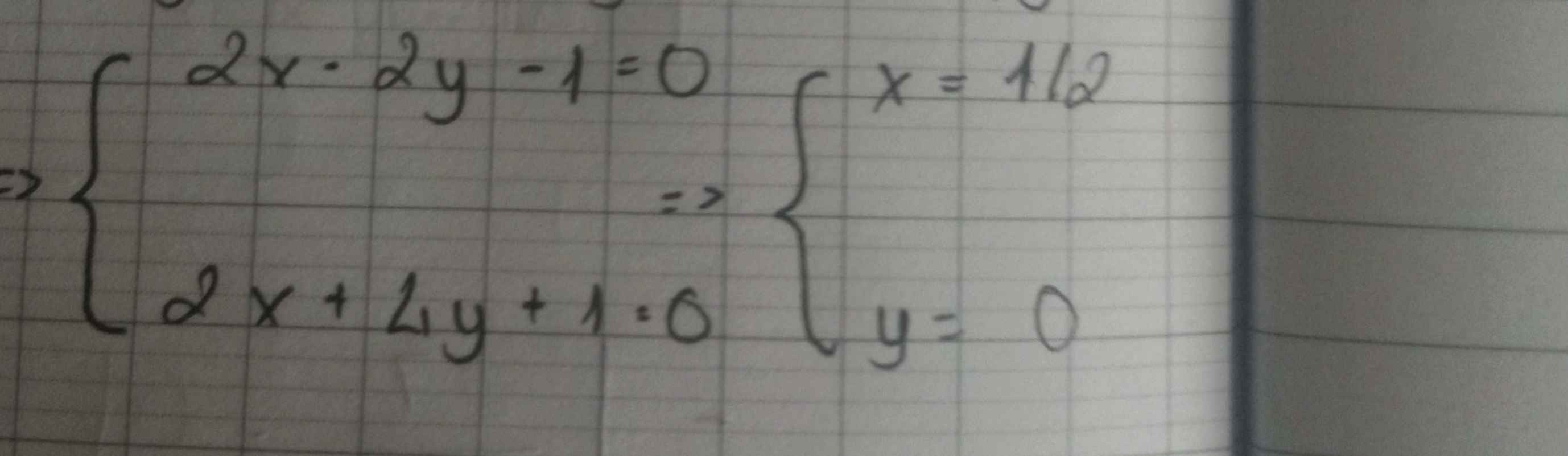







Δ vuông góc d3
=>Δ: x+2y+c=0
Tọa độ giao của(d1) và (d2) là;
x+3y=1 và x-3y=5
=>x=3 và y=-2/3
Thay x=3 và y=-2/3 vào Δ, ta được:
c+3-4/3=0
=>c=-5/3