Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(Pytago:\)
\(AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+9^2}=15\left(cm\right)\)
\(CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16\left(cm\right)\)
=> C


a) Xét \(\Delta BAD\) và \(\Delta BCE:\)
\(\widehat{B}chung.\)
\(\widehat{D}=\widehat{E}\left(=90^o\right).\)
\(\Rightarrow\Delta BAD\sim\Delta BCE\left(g-g\right).\)
b) Xét \(\Delta ABC:\)
CE là đường cao \(\left(CE\perp AB\right).\)
AD là đường cao \(\left(AD\perp BC\right).\)
Mà F là giao điểm của CE và AD.
\(\Rightarrow BF\) là đường cao.
Xét \(\Delta ABC\) cân tại B:
BF là đường cao (gt).
\(\Rightarrow BF\) là phân giác \(\widehat{ABC}.\)

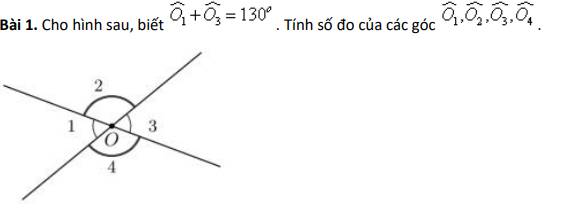
Do \(\widehat{O_1}\) và \(\widehat{O_3}\) là 2 góc đối đỉnh
\(\Rightarrow\widehat{O_1}=\widehat{O_3}=\dfrac{130^o}{2}=65^o\\ \Rightarrow\widehat{O_2}=\widehat{O_4}=180^o-65^o=115^o\)

Khoảng cách giữa các số hạng là 2
Số các số hạng là: ( 2n +1 - 1 ) : 2 + 1 = n + 1 ( số hạng )
Tổng S = ( 2n + 1 + 1 ) ( n + 1 ) : 2 = ( 2n + 2 ) ( n + 1 ) : 2 = 2 ( n + 1 ) ( n + 1 ) : 2 = ( n + 1 ) ( n + 1 ) = ( n + 1)2

Số đo góc chưa chính xác :(
Gọi giao điểm của \(BM\) và \(CN\)là \(O\)
Từ \(O\)kẻ \(OH\)là phân giác \(\widehat{BOC}\)\(\left(H\in BC\right)\)
Xét \(\Delta ABC\)có:
\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^o\) (định lí tổng ba góc \(\Delta\))
\(\Rightarrow\widehat{ABC}+\widehat{ACB}=180^o-60^o=120^o\)
Ta có:
\(\widehat{OBC}=\widehat{OBA}=\frac{\widehat{ABC}}{2}\) (\(OB\): phân giác \(\widehat{ABC}\))
\(\widehat{OCB}=\widehat{OCA}=\frac{\widehat{ACB}}{2}\) (\(OC\): phân giác \(\widehat{ACB}\))
\(\Rightarrow\widehat{OBC}+\widehat{OCB}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{120^o}{2}=60^o\)
Xét \(\Delta BOC\)có:
\(\widehat{OBC}+\widehat{OCB}+\widehat{BOC}=180^o\) (định lí tổng ba góc \(\Delta\))
\(\Rightarrow\widehat{BOC}=180^o-60^o=120^o\)
Ta có:
\(\widehat{BOH}=\widehat{HOC}=\frac{\widehat{BOC}}{2}=\frac{120^o}{2}=60^o\) (\(OH\): phân giác \(\widehat{BOC}\))
Ta có:
\(\widehat{BOC}+\widehat{BON}=180^o\) (kề bù)
\(\Rightarrow\widehat{BON}=180^o-120^o=60^o\)
\(\Rightarrow\widehat{BON}=\widehat{BOH}\left(=60^o\right)\)
Ta có:
\(\widehat{BOC}+\widehat{COM}=180^o\) (kề bù)
\(\Rightarrow\widehat{COM}=180^o-120^o=60^o\)
\(\Rightarrow\widehat{COM}=\widehat{HOC}\left(=60^o\right)\)
Xét \(\Delta BON\)và \(\Delta BOH\)có:
\(\widehat{OBN}=\widehat{OBH}\) (\(OB\): phân giác \(\widehat{ABC}\))
\(OB\): chung
\(\widehat{BON}=\widehat{BOH}\) (cmt)
\(\Rightarrow\Delta BON=\Delta BOH\left(g.c.g\right)\)
\(\Rightarrow BN=BH\) (2 cạnh tương ứng)
Xét \(\Delta COM\)và \(\Delta COH\)có:
\(\widehat{COM}=\widehat{COH}\) (cmt)
\(OC\) : chung
\(\widehat{MCO}=\widehat{HCO}\) (\(OC\): phân giác \(\widehat{ACB}\))
\(\Rightarrow\Delta COM=\Delta COH\left(g.c.g\right)\)
\(\Rightarrow MC=HC\) (2 cạnh tương ứng)
Ta có:
\(BC=BH+HC\)
Mà \(\hept{\begin{cases}BN=BH\\MC=HC\end{cases}}\)
\(\Rightarrow BC=BN+MC\left(đpcm\right)\)

Bằng những dẫn chứng cụ thể, phong phú, giàu sức thuyết phục trong lịch sử dân tộc và cuộc kháng chiến chống thực dân Pháp xâm lược, bài văn đã làm sáng tỏ một chân lí: “Dân ta có một lòng nồng nàn yêu nước. Đó là một truyền thống quý báu của ta”
Học tốt
Nội dung :
Bằng những dẫn chứng cụ thể,phong phú,giàu sức thuyết phục trong lịch sử dân tộc và cuộc kháng chiến chống thực dân pháp xâm lược,bài văn đã làm sáng tỏ một chân lí:''dân ta có một lòng nồng nàn yêu nước.dó là truyền thống quý báu của ta''.
Hok tốt