Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\int_0^1(2-\dfrac{2}{x+1})dx\)
\(=\int_0^12dx-\int_0^1\dfrac{2}{x+1}dx\)
\(=2x|_0^1-\int_0^1\dfrac{2}{x+1}d(x+1)\)
\(=2x|_0^1-2.\ln(x+1)|_0^1\)
\(=2-2\ln 2\)

Giải như sau:
Ta biết rằng \(d\left(u\left(x\right)\right)=u\left(x\right)'d\left(x\right)\)
\(\Rightarrow\int\frac{x}{2-x^2}dx=\frac{1}{2}\int\frac{d\left(x^2\right)}{2-x^2}=-\frac{1}{2}\int\frac{d\left(2-x^2\right)}{2-x^2}=-\frac{1}{2}ln\left|2-x^2\right|+c\)
P/s: Muốn tính nguyên hàm mà tử nhỏ hơn mẫu thứ nhất bạn có thể phan tích mẫu ra thành các nhân tử có bậc nhỏ như bậc của tử số, rồi từ đó đặt ẩn phụ hoặc tách ghép hợp lý. Thứ 2 là bạn có thể sử dụng phương pháp $d(u(x))=u(x)'dx$ để đưa ẩn về cùng một mối ( như cách mình giải bài này). Nói chung mình diễn đạt có thể không rõ ràng một chút nhưng chủ yếu bạn làm nhiều tìm tòi nhiều sẽ quen thôi :)

1) bạn dùng dấu U
điều kiện \(\begin{cases}m\ne0,m>-\frac{1}{4}\\m< 1\end{cases}\)
muons dễ nhìn thì vẽ trục số:
=> điều kiện x \(\in\left(-\frac{1}{4};1\right)\backslash\left\{0\right\}\)

Gọi tử là x
Mẫu là 105-x
Theo đề, ta có:
\(\dfrac{x}{105-x}=\dfrac{60}{165}=\dfrac{4}{11}\)
=>11x=420-4x
=>15x=420
hay x=28
Vậy: Phân số cần tìm là 28/77
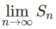 và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.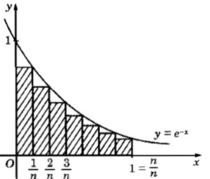
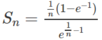
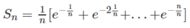
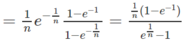
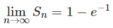
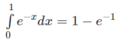
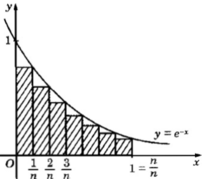
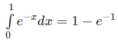

lấy tử chia cho mẫu => tách ra làm bình thương thôi
nói ((((((chay)))))) thế này thì khó nói lắm