Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
+ Để vật dao động với cơ năng cực đại khi Amax.
+ x = x1 + x2 => x1 = x – x2 = A cos(ωt – π/3) - A2 cos(ωt – π/2)
= A cos(ωt – π/3) + A2 cos(ωt + π/2)
+ A12 =102 = A2 + A22 + 2AA2cos(- π/3 - π/2).
ó A22 - AA2√3-100 + A2 = 0 (1).
+ Để phương trình (1) có nghiệm đối với A2 <=> Δ = (-A√3)2 – 4.1.(-100 + A2) ≥ 0
=> 0 ≤ A ≤ 20 cm.
=> Amax = 20 thay vào (1) tìm được A2 = 10√3 cm.

Chu kì dao động: T = 2π/ω = 2π/5π = 0,4s
Thời điểm t = 0 và thời điểm độ lớn lực đàn hồi bằng 0,5N được biểu diễn trên đường tròn lượng giác:
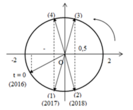
Một chu kì có 4 lần độ lớn lực đàn hồi bằng 0,5N
Sau 504T độ lớn lực đàn hồi bằng 0,5N lần thứ 2016
=> Lực đàn hồi có độ lớn bằng 0,5N lần thứ 2018 vào thời điểm:
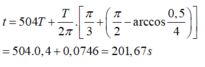
Đáp án C

Chọn đáp án D
@ Lời giải:
+ Thế năng của vật dao động điều hòa biến thiên tuần hoàn với tần số góc:
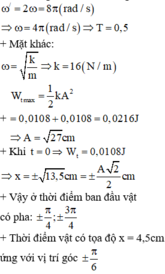
+ Vậy thời điểm vật qua vị trí x = 4,5cm lần đầu tiên là: T 24 = 1 48 s

Chọn A
Vật dao động điều hòa có phương trình x = A cos ω t + φ có pha dao động

Năng lượng dao động bằng động năng hoặc cơ năng cực đại:
\(W=\dfrac{1}{2}m.v_{max}^2=\dfrac{1}{2}m.\omega^2.A^2=0,5.0,5.(10\pi)^2.0,02^2=0,01J\)

Chọn đáp án A
@ Lời giải: