Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
@ Lời giải:
![]()
+ Ban đầu vật ở biên dương
+ Vị trí vật có li độ x = -4cm ngược chiều dương ứng với góc 1200
+ Thời gian vật đi qua vị trí x = -4cm theo chiều dương lần thứ 2 là:
![]()

Chọn đáp án D
@ Lời giải:
+ Thế năng của vật dao động điều hòa biến thiên tuần hoàn với tần số góc:
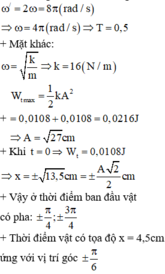
+ Vậy thời điểm vật qua vị trí x = 4,5cm lần đầu tiên là: T 24 = 1 48 s

Lời giải:
Vì tại thời điểm ban đầu vật đang qua VTCB theo chiều âm nên phương trình dao động của vật \(x=A\cos\left(\omega t+\frac{\pi}{2}\right)\) (cm)
Từ điều kiện đề bài kết hợp với công thức \(A^2=x^2+\left(\frac{v}{\omega}\right)^2\) nên \(\omega=2\pi\Rightarrow A=5\left(cm\right)\)
Do đó phương trình là \(x=5\cos\left(2\pi t+\frac{\pi}{2}\right)\left(cm\right)\)

Chu kì dao động: T = 2π/ω = 2π/5π = 0,4s
Thời điểm t = 0 và thời điểm độ lớn lực đàn hồi bằng 0,5N được biểu diễn trên đường tròn lượng giác:
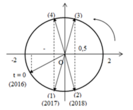
Một chu kì có 4 lần độ lớn lực đàn hồi bằng 0,5N
Sau 504T độ lớn lực đàn hồi bằng 0,5N lần thứ 2016
=> Lực đàn hồi có độ lớn bằng 0,5N lần thứ 2018 vào thời điểm:
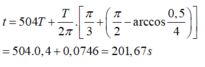
Đáp án C

Phương pháp: Khoảng cách giữa hai điểm sáng được biểu diễn bởi phương trình:
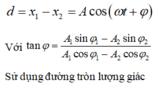
Cách giải:
+ Phương trình vận tốc của hai chất điểm:
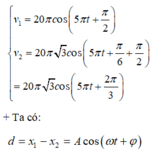
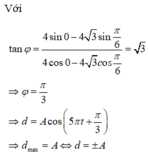
+ Thời điểm đầu tiên t hai điểm sáng cách xa nhau nhất được biểu diễn trên đường tròn lượng giác
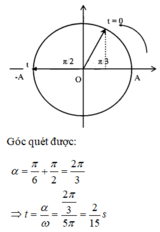
+ Tại t = 2/15s tỉ số vận tốc của chất điểm 1 so với chất điểm 2:
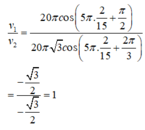
Đáp án A

Phương pháp: Hai vật có cùng li độ khi x1 = x2
Cách giải:
Tần số góc của con lắc lò xo 1 và 2:
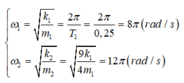
Theo bài ra ta có phương trình dao động của con lắc 1 và 2:
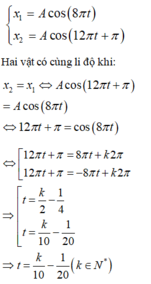
Hai vật có cùng li độ lần thứ 2018 ứng với k = 2018
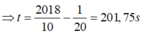
Đáp án A


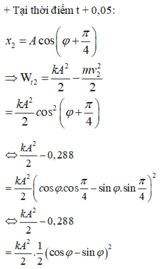


Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác:

Đáp án D

M N 10 -10 5 O
Biểu diễn dao động bằng véc tơ quay như hình vẽ. Vật qua li độ 5cm theo chiều âm --> véc tơ quay qua N.
Lần thứ 2 --> véc tơ xuất phát từ M (ban đầu), quay hết 1 vòng rồi quay tiếp đến N
Thời gian: \(t=T+\frac{60}{360}T=\frac{7}{6}T=\frac{7}{6}.2=\frac{7}{3}s\)
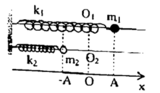
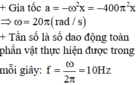
Ta có `505T` thì `2020` lần vật đi qua vị trí cách vị trí cân bằng `4 cm`.
`=>\Delta t_[2021]=t_1 +505T=T/12 +505T`
`=6061/12 T=6061/12 .[2\pi]/[\pi]=6061/6 (s)`.