Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(s_2-s_1=40\Leftrightarrow s-s_1-s_1=40\Leftrightarrow s-2s_1=40\)
\(\Rightarrow\dfrac{1}{2}gt^2-2\cdot\dfrac{1}{2}gt_1^2=40\)
Mà: \(t_1=\dfrac{1}{2}t\Rightarrow\dfrac{1}{2}gt^2-2\cdot\dfrac{1}{2}g\left(\dfrac{1}{2}t\right)^2=40\)
\(\Leftrightarrow\dfrac{1}{4}gt^2=40\Leftrightarrow t=\sqrt{\dfrac{40}{\dfrac{1}{4}g}}=\sqrt{\dfrac{40}{\dfrac{1}{4}\cdot10}}=4\left(s\right)\)
\(\Rightarrow\left\{{}\begin{matrix}h=s=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot4^2=80\left(m\right)\\v=gt=10\cdot4=40\left(m/s\right)\end{matrix}\right.\)
Vậy: h = 80 (m), t = 4 (s) và v = 40 (m/s).

Quãng đường vật rơi nửa thời gian đầu:
![]()
Quãng đường vật rơi nửa thời gian cuối
![]()
Quãng đường vật rơi: h = h 1 + h 2
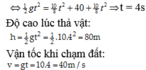

Đáp án A
Quãng đường vật rơi trong 3 giây đầu:
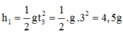
Quãng đường vật rơi trong 2 giây đầu:
![]()
Quãng đường vật rơi trong giây thứ 3:
![]()
![]()
Mà
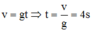
Độ cao lúc thả vật:
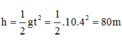

Quãng đường vật rơi trong 3 giây đầu:
![]()
Quãng đường vật rơi trong 2 giây đầu:
![]()
Quãng đường vật rơi trong giây thứ 3:
![]()
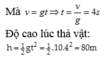

Gọi thời gian rơi nửa quãng đường sau là \(t(s)\), thì thời gian rơi nửa quãng đường đầu là \(t+1\)
Theo đề bài ta có:
\(\dfrac{h}{2}=\dfrac{1}{2}.g.(t+1)^2\Rightarrow h = g(t+1)^2\) (1)
\(h=\dfrac{1}{2}.g.(t+t+1)^2\Rightarrow h=\dfrac{1}{2}.g.(2t+1)^2\) (2)
Từ (1) và (2) suy ra: \( g(t+1)^2 = \dfrac{1}{2}g.(2t+1)^2\)
\(\Rightarrow t^2+2t+1= \dfrac{1}{2}(4t^2+4t+1)\)
\(\Rightarrow t^2 = \dfrac{1}{2}\)
\(\Rightarrow t = \dfrac{1}{\sqrt 2}(s)\)
Suy ra:
Độ cao: \(h = g(t+1)^2=10.(\dfrac{1}{\sqrt 2}+1)^2\approx 29,1 (m)\)
Thời gian chạm đất: \(t_1= 2.t+1=\sqrt 2 + 1 \approx 2,41 (s)\)
Tốc độ khi chạm đất: \(v=g.t=10.2,41=24,1(m/s)\)




Đáp án D
Quãng đường vật rơi nửa thời gian đầu:
Quãng đường vật rơi nửa thời gian cuối
Quãng đường vật rơi:
Độ cao lúc thả vật:
Vận tốc khi chạm đất:
v = gt = 10.4 = 40m/s