Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

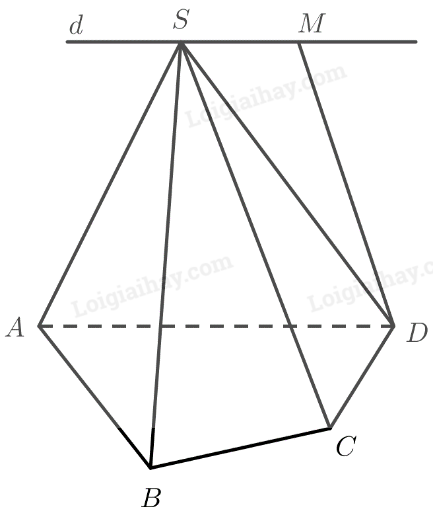
\(A{\rm{D}}M{\rm{S}}\) là hình thang có hai đáy là \(A{\rm{D}}\) và \(M{\rm{S}}\) nên \(A{\rm{D}}\parallel M{\rm{S}}\).
Theo đề bài ta lại có \(d\parallel A{\rm{D}}\).
Do đó \(d \equiv MS\) (theo định lí 1).
Lại có: \(SM \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {SA{\rm{D}}} \right)\).

THAM KHẢO:

CD//AB nên góc giữa SB và CD là góc giữa AB và SB, \(\widehat{ABS}\)
CB//AD nên góc giữa SD và CB là góc giữa SD và AD, \(\widehat{ADS}\)
Ta có: tan\(\widehat{ABS}\)=tan\(\widehat{ADS}\)=\(\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
Suy ra \(\widehat{ABS}\)=\(\widehat{ADS}\)=\(\dfrac{\pi}{3}\)

Gọi \(O\) là tâm của đáy \( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot B{\rm{D}}\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(\left. \begin{array}{l} \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\\B{\rm{D}} \subset \left( {MB{\rm{D}}} \right)\end{array} \right\} \Rightarrow \left( {MB{\rm{D}}} \right) \bot \left( {SAC} \right)\)
Chọn B.

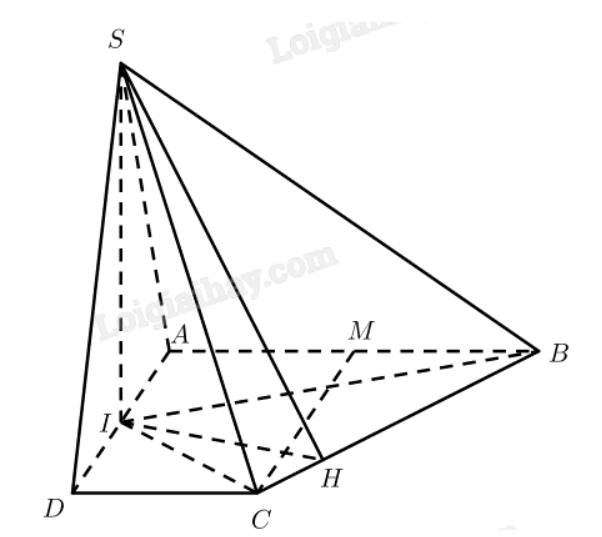
\(\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)\)
Kẻ \(IH \bot BC\left( {H \in BC} \right)\)
\(SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC\)
\( \Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {AHI}\) là góc nhị diện \(\left[ {S,BC,A} \right]\)\( \Rightarrow \widehat {AHI} = {60^ \circ }\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} - {S_{AIB}} - {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}\)
Gọi \(M\) là trung điểm của \(AB\)
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}} = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}\)

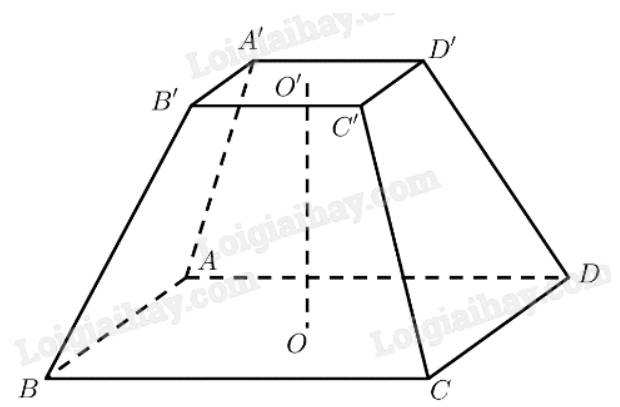
Diện tích đáy lớn là: \(S = A{B^2} = {3^2} = 9\)
Diện tích đáy bé là: \(S' = {2^2} = 4\)
Thể tích hình chóp cụt là:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.4\left( {9 + \sqrt {9.4} + 4} \right) = \frac{{76}}{3} \approx 25,3\left( {d{m^3}} \right)\)

tham khảo:

Gọi I là trung điểm của BD.
Tam giác BCD có IM là đường trung bình nên IM//DC và IM=\(\dfrac{1}{2}\)CD=\(\dfrac{1}{2}\).2a=1
Tam giác ABD có IN là đường trung bình nên IN//AB và IN=\(\dfrac{1}{2}\)AB=\(\dfrac{1}{2}\).2a=1
Ta có: cos\(\widehat{MIN}\)=\(\dfrac{a^2+a^2-\left(a\sqrt{3}\right)^2}{2.a.a}=\dfrac{-1}{2}\)
Nên \(\widehat{MIN}\)=\(120^0\)
Do AB//IN, CD//IM nên góc giữa AB và CD là góc giữa IM và IN là bằng \(120^0\)

Tham khảo hình vẽ:
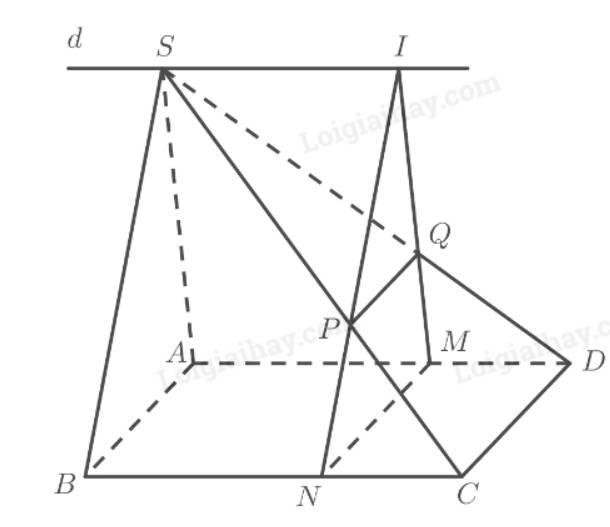
a) Ta có:
\(\begin{array}{l}MN = \left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {SC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\PQ = \left( \alpha \right) \cap \left( {SC{\rm{D}}} \right)\\MN\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel C{\rm{D}}\parallel PQ\).
\( \Rightarrow MNPQ\) là hình bình hành.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in MQ \Rightarrow I \in \left( {SA{\rm{D}}} \right)\\I \in NP \Rightarrow I \in \left( {SBC} \right)\end{array} \right\} \Rightarrow I \in \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\ \Rightarrow SI = \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC\parallel A{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(A{\rm{D}}\parallel BC\parallel SI\).
Vậy \(I\) luôn luôn thuộc đường thẳng \(d\) đi qua \(S\) song song với \(AD\) và \(BC\) cố định khi \(M\) di động trên \(AD\).

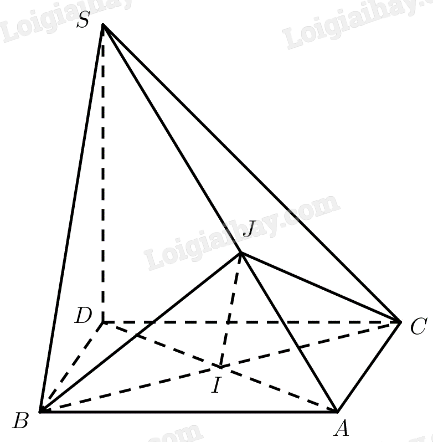
a) \(ABC{\rm{D}}\) là hình thoi \( \Rightarrow A{\rm{D}} \bot BC\)
\(S{\rm{D}} \bot \left( {ABC} \right) \Rightarrow S{\rm{D}} \bot BC\)
\(\left. \begin{array}{l} \Rightarrow BC \bot \left( {SA{\rm{D}}} \right)\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
b) Kẻ \(IJ \bot SA\left( {J \in SA} \right)\).
\(\Delta ABC\) đều \( \Rightarrow AI = \frac{{a\sqrt 3 }}{2} \Rightarrow A{\rm{D}} = 2AI = a\sqrt 3 \)
\(\Delta SAD\) vuông tại \(D\) \( \Rightarrow S{\rm{A}} = \sqrt {S{D^2} + A{{\rm{D}}^2}} = \frac{{3a\sqrt 2 }}{2}\)
Tam giác \(BCJ\) có \(IJ\) là trung tuyến và \(IJ = \frac{1}{2}BC\)
Vậy tam giác \(BCJ\) vuông tại \(J \Rightarrow BJ \bot JC\)
\(\begin{array}{l}\left. \begin{array}{l}BC \bot \left( {SA{\rm{D}}} \right) \Rightarrow BC \bot SA\\IJ \bot SA\end{array} \right\} \Rightarrow SA \bot \left( {BCJ} \right)\\\left. \begin{array}{l} \Rightarrow SA \bot BJ\\BJ \bot JC\end{array} \right\} \Rightarrow BJ \bot \left( {SAC} \right)\end{array}\)
Mà \(BJ \subset \left( {SAB} \right)\)
Vậy \(\left( {SAB} \right) \bot \left( {SAC} \right)\).

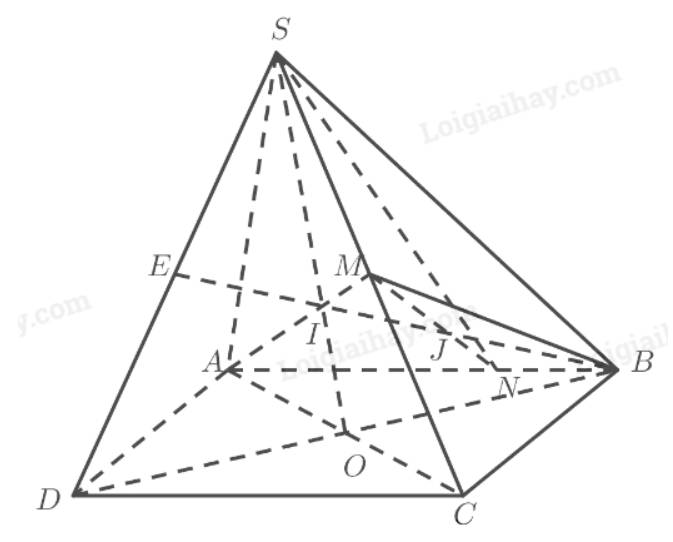
a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(I\) là giao điểm của \(AM\) và \(SO\). Ta có:
\(\left. \begin{array}{l}I \in SO \subset \left( {SB{\rm{D}}} \right)\\I \in AM\end{array} \right\} \Rightarrow I = AM \cap \left( {SB{\rm{D}}} \right)\)
Xét tam giác \(SAC\) có:
\(ABCD\) là hình bình hành \( \Rightarrow O\) là trung điểm của \(AC\)
Theo đề bài ta có \(M\) là trung điểm của \(SC\)
Mà \(I = SO \cap AM\)
\( \Rightarrow I\) là trọng tâm của .
b) Gọi \(E\) là giao điểm của \(S{\rm{D}}\) và \(BI\). Ta có:
\(\left. \begin{array}{l}E \in BI \subset \left( {ABM} \right)\\E \in S{\rm{D}}\end{array} \right\} \Rightarrow E = S{\rm{D}} \cap \left( {ABM} \right)\)
c) Gọi \(J\) là giao điểm của \(MN\) và \(BE\). Ta có:
\(\left. \begin{array}{l}J \in BE \subset \left( {SB{\rm{D}}} \right)\\J \in MN\end{array} \right\} \Rightarrow J = MN \cap \left( {SB{\rm{D}}} \right)\)

a) Khi a = 1dm:
Diện tích một mặt `(S) = a^2 = 1^2 = 1dm^2`
Thể tích `(V) = a^3 = 1^3 = 1dm^3`
Khi a = 3dm:
Diện tích một mặt `(S) = a^2 = 3^2 = 9dm^2`
Thể tích `(V) = a^3 = 3^3 = 27dm^3`
b) Để S = `25dm^2`, ta cần tìm giá trị của a. Ta có:
`a^2 = 25`
=> `a = √25 = 5dm`
c) Để V = `64dm^3`, ta cần tìm giá trị của a. Ta có:
`a^3 = 64`
=> `a = ∛64 = 4dm`