Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B.
• Kí hiệu số ghế là 1;2;3;4;5;6.
• Xếp trước 3 nam ngồi ở vị trí số lẻ và 3 nữ ngồi ở vị trí số chẳn và ngược lại
Ta có: 3 ! . 3 ! . 2 ! = 72

Đáp án B

Số cách xếp 10 học sinh vào 10 ghế là: 10!
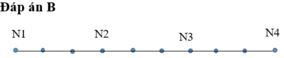
4 bạn nữ chỉ có thể xếp vào các vị trí N1,N2,N3,N4
Nếu Huyền ở vị trí N1 thì có 3! cách xếp 3 bạn nữ còn lại, Quang có 5 cách chọn chỗ ngồi và có 5! cách xếp 5 bạn nam còn lại. Vậy có 3!.5.5! = 3600 cách xếp
Tương tự nếu Huyền ở vị trí N4 cũng có 3600 cách xếp
Nếu Huyền ở vị trí N2 thì có 3! cách xếp 3 bạn nữ còn lại, Quang có 4 cách chọn chỗ ngồi và có 5! cách xếp 5 bạn nam còn lại. Vậy có 3!.4.5! = 2880 cách xếp
Tương tự nếu Huyền ở vị trí N3 cũng có 2880 cách xếp
Vậy có 2(3600 + 2880) = 12960 cách xếp thỏa mãn đề bài
⇒ p = 12960 10 ! = 1 280

Số cách xếp 10 học sinh vào 10 ghế là: 10!
4 bạn nữ chỉ có thể xếp vào các vị trí N1,N2,N3,N4
Nếu Huyền ở vị trí N1 thì có 3! cách xếp 3 bạn nữ còn lại, Quang có 5 cách chọn chỗ ngồi và có 5! cách xếp 5 bạn nam còn lại. Vậy có 3!.4.5! = 2880 cách xếp
Tương tự nếu Huyền ở vị trí N4 cũng có 3600 cách xếp
Nếu Huyền ở vị trí N2 thì có cách xếp 3 bạn nữ còn lại, Quang có 4 cách chọn chỗ ngồi và có cách xếp 5 bạn nam còn lại. Vậy có 2(3600 + 2880)= 12960 cách xếp
Tương tự nếu Huyền ở vị trí N3 cũng có 2880 cách xếp
Vậy có cách xếp thỏa mãn đề bài
⇒ p = 12960 10 ! = 1 280

Chọn đáp án A
Kí hiệu Nam: l và Nữ: ¡. Ta có
Có 2 trường hợp Nam, nữ ken kẽ nhau và 4 trường hợp hai bạn Nữ ngồi cạnh nhau.
Trường hợp 1. Nam nữ ngồi xen kẽ nhau gồm:
Nam phía trước: l¡l¡l¡l¡l¡.
Nữ phía trước: ¡l¡l¡l¡l¡l.
Trường hợp 2. Hai bạn nữ ngồi cạnh nhau: l¡¡l¡l¡l¡l Hoặc
l¡l¡¡l¡l¡l. Tương tự ta có thêm 2 trường hợp nữa. Các bước xếp như sau:
B1: Xếp 5 bạn nam. B2: Xếp cặp Tự - Trọng. B3: Xếp các bạn nữ còn lại. Khi đó số kết quả xếp cho 2 trường hợp trên như sau:


Xét 2 khả năng:
+) Trường hợp ở giữa có 3 ghế có thể xếp nam ở bên phải hoặc trái nên số cách xếp
là 2 . 4! . 2! = 96
+) Trường hợp ở giữa có 2 ghế thì ghế ngoài cùng bên phải hoặc bên trái sẽ trống. Tương ứng số cách sắp xếp là 2 . 2 . 4! . 2! = 192
Vậy số cách sắp xếp là 192 + 96 = 288
Đáp án cần chọn là C

chọn đc 5 em học sinh có đúng 2 nữ vậy sẽ có 3 nam
số cách chọn đc là:\(C^2_6.C^3_8\)


Chọn C.
Ta coi 3 bạn nữ là vị trí thì số cách sắp xếp 6 là 6!, sau đó xếp 3 bạn nữ vào vị trí đó là 3! Nên số cách sắp xếp là 6!.3!