Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc ban đầu là x km/h (x>o).
Với vận tốc này thì thời gian để đi quãng đường 30 km:
30/x(h)
Vì với vận tốc này sẽ đến B chậm mất nửa giờ hay chậm mất 1/2 h, nên suy ra thời gian dự định đến B sẽ là:
30/x - 1/2(h) (1)
Nếu tăng vận tốc thêm 5 km/h thì vận tốc mới sẽ là:
x + 5(km/h)
Với vận tốc mới thì thời gian đi hết 30 km sẽ là:
30/(x + 5)...(h)
Thời gian này so với thời gian dự định là sớm hơn nửa giờ (hay 1/2 h), nên suy ra thời gian dự định sẽ là:
30/(x + 5) +1/2 (h) (2)
Vì (1) bằng (2) nên ta có:
30/x - 1/2 = 30/(x + 5) +1/2
=> x^2 + 5x - 150 = 0
Giải phương trình trên ta có:
x1 = 10 (nhận)
x2 = - 15 (loại)
Vậy vận tốc ban đầu là 10 km/h.
Gọi v là vận tốc lúc đầu, t là thời gian chạy đoạn đường 30km.
Ta có: vt = 30 (1)
Người đó nhận thấy rằng sẽ đến B chậm mất nửa giờ nửa giữ nguyên vận tốc đang đi. Nhưng nếu tăng tốc thêm 5 km/h thì sẽ tới đích sớm hơn nửa giờ. => có nghĩa là nếu tăng v thêm 5 thì sẽ đi nhanh hơn 0.5 + 0.5 = 1h
Vậy ta có: (v + 5)(t - 1) = 30 (2)
Cho (1) = (2) => vt = vt + 5t - v - 5 <=> 5t - v - 5 = 0
thay t = 30/v vào ta có:
150/v - v - 5 =0
<=> 150 - 5v - v*v = 0
Lấy máy bấm => v = 10 (nhận) hoặc v = -15 (loại)

Gọi v là vận tốc lúc đầu , t là thời gian chạy đoạn đường 30km.
ta có v.t=30(*)
Sẽ đến B chậm mất nữa giờ nếu giữ nguyên vận tốc đang đi,nhưng nếu tăng vận tốc thêm 5km/h thì tới B sớm hơn nửa giờ , tức là tăng v thêm 5 thí sẽ đi nhanh hơn 0.5+0.5=1h,
Vậy ta có : (v+5)(t-1)=30(**)
Cho (*)=(**) ta có : vt=vt+5t-v-5 <=> 5t-v-5=0
Thay \(t=\frac{30}{v}\) vào ta có : \(\frac{150}{v}-v-5=0\Leftrightarrow-v^2-5v+150=0\Leftrightarrow\hept{\begin{cases}v=10\\v=-15\left(loai\right)\end{cases}}\)
Gọi x là vận tốc xe đạp trên quãng đường đã đi lúc đầu (x>0) (km/h)
y là độ dài quãng đường AB (y>30) (km)
Theo đề bài : \(\hept{\begin{cases}\frac{30}{x}=\frac{y-30}{x}+\frac{1}{2}\left(1\right)\\\frac{30}{x+5}=\frac{y-30}{x}-\frac{1}{2}\left(2\right)\end{cases}}\)
Lấy (1) trừ (2) theo vế được : \(\frac{30}{x}-\frac{30}{x+5}=1\) Giải phương trình này được x = 10 (nhận ) và x = -15 (loại)
Vậy : Vận tốc xe đạp trên quãng đường đã đi lúc đầu là 10 km/h

Gọi vận tốc của người đi xe đạp là a(km/h) \((a>0)\)
Theo đề,ta có: \(\dfrac{30}{a}-1=\dfrac{30}{a+5}\)
\(\Leftrightarrow\)\(\dfrac{30-a}{a}=\dfrac{30}{a+5}\Rightarrow\left(30-a\right)\left(a+5\right)=30a\)
\(\Leftrightarrow30a+150-a^2-5a=30a\Leftrightarrow a^2+5a-150=0\)
\(\Leftrightarrow\left(a-10\right)\left(a+15\right)=0\)
mà \(a>0\Rightarrow a=10\)
Vậy vận tốc của người đi xe đạp là 10km/h

gọi v là vận tốc bđ
thời gian dự đinh là 50/y
qđ còn lại sau khi đi dk 2h là 50-2v
thời gian đi qđ còn lại là 50-2v/(v+2)
từ giả thiết đề bài cho ta có pt
50-2v/(v+2)+2+30/60=50/v
bạn tự giải pt nha mk hướng dẫn tek thui

Gọi vận tốc dự định đi của người đó là x (km/h) (x > 0)
Thời gian dự định đi của người đó là 36/x (h)
Thời gian người đó đi nửa quãng đường đầu là 18/x (h)
Nửa quãng đường sau người đó đi với vận tốc là x + 2 (km/h) và thời gian người đó đi là 18/(x+2) (h)
Vì nghỉ lại 30 phút nên thời gian đi từ lúc xuất phát đến khi tới B là 18 x + 1 2 + 18 x + 2
Do người đó đến B chậm hơn dự kiến 12 phút = 1/5h nên ta có phương trình:
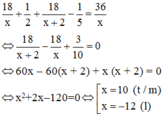
Vậy vận tốc của người đi xe đạp trên đoạn đường cuối của đoạn AB là 12 km/h
Đáp án: A
Gọi vận tốc ban đầu là x km/h (x > 0).
Với vận tốc này thì thời gian để đi quãng đường 30 km:
30/x(h)
Vì với vận tốc này sẽ đến B chậm mất nửa giờ hay chậm mất 1/2 h, nên suy ra thời gian dự định đến B sẽ là:
30/x - 1/2(h) (1)
Nếu tăng vận tốc thêm 5 km/h thì vận tốc mới sẽ là:
x + 5(km/h)
Với vận tốc mới thì thời gian đi hết 30 km sẽ là:
30/(x + 5)(h)
Thời gian này so với thời gian dự định là sớm hơn nửa giờ (hay 1/2 h), nên suy ra thời gian dự định sẽ là:
30/(x + 5) +1/2(h) (2)
Vì (1) bằng (2) nên ta có:
30/x - 1/2 = 30/(x + 5) +1/2
=> x^2 + 5x - 150 = 0
Giải phương trình trên ta có:
x1 = 10 (nhận)
x2 = -15 (loại)
=> Vận tốc ban đầu là 10 km/h.