Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (km/h) là vận tốc dự định của người đó (x>5)
Vận tốc người đó giảm vận tốc 5km/h là x−5 (km/h)
Thời gian dự đinh đi là: \(\dfrac{60}{x}\)(giờ)
Thời gian thực tế người đó đi nửa quãng đường đầu là: \(\dfrac{30}{x}\)(giờ)
Thời gian thức tế người đó đi nửa quãng đường còn lại là: \(\dfrac{30}{x-5}\)(giờ)
Theo đề ra ta có thời gian thực tế chậm hơn thời gian dự định là 1 giờ nên ta có:
\(\dfrac{60}{x}\)=\(\dfrac{30}{x}\)+ \(\dfrac{30}{x-5}\) - 1
⇒ 60(x-5) = 30(x-5) + 30x - x(x-5)
⇔ 60x - 300 = 30x - 150 + 30x - x2+5x
⇔ x2 - 5x - 150 = 0
⇔ \(\left[{}\begin{matrix}x=15\left(tm\right)\\x=-10\left(loại\right)\end{matrix}\right.\)
Vậy.....

Gọi quãng đường AB là: x ( x > 0 ) ( km)
Thời gian dự định đi hết quãng đường AB là: y ( y > 0 ) ( giờ )
\(\Rightarrow\)10y = x
\(\Leftrightarrow\)x - 10y = 0 ( 1 )
Thời gian thực tế đế người đi xe đạp đi hết nửa quãng đường là: \(\frac{x}{2}:10=\frac{x}{20}\)
Vì muốn đến B kịp giờ nên người ấy phải đi với vânkj tốc 15km/h trên quãng đường còn lại nên =) Thời gian để đi hết quãng đường còn lai là: \(\frac{x}{2}:15=\frac{x}{30}\)giờ
Vì thời gian dự định bằng thời gian thực tế và người đó nghỉ 0,5 giờ ( 30 phút )
\(\Rightarrow\)\(\frac{x}{20}+\frac{x}{30}+0,5=y\)
\(\Leftrightarrow\)\(\frac{x}{12}-y=0,5\)( 2 )
Từ ( 1 ) và ( 2 ) ta có hệ phương trình:
\(\hept{\begin{cases}x-10y=0\\\frac{x}{12}-y=-0,5\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x=30\\y=3\end{cases}}\)
Vậy quãng đường AB: 30km

Gọi độ dài quãng đường \(AB\) là: \(a\left(km\right)\left(a>0\right)\)
Gọi thời gian dự định ban đầu là:\(b\left(h\right)\left(b>0\right)\)
Ta có: \(10b=a\)
\(\Rightarrow10b-a=0\)
Người đó đi được nửa đường thì hết số thời gian:
\(\frac{0,5a}{10}=0,05a\)
Còn lại số thời gian:
\(b-0,05a-0,5\)
\(\Rightarrow15\left(b-0,05a-0,5\right)=0,5a\)
\(\Rightarrow15b-1,25a=7,5\)
Từ đó ta có hệ phương trình sau:
\(10b-a=0\)
\(\Leftrightarrow15b-1,25a=7,5\)\(\Leftrightarrow\hept{\begin{cases}a=30\\b=3\end{cases}}\)
Vậy \(s_{AB}=30km\)

đáp án là 10km/h
Gợi ý: ta có pt là
20/a + 1/4 = 1 + (20-a)/(a-2)
Trong đó:
a là vận tốc dự định
20/a là thời gian dự định
1/4 là 15p
(20-a)/(a-2) là thời gian đi trong quãng đường còn lại
Khai triển pt ta sẽ có:
4(a^2-40) = 3(a^2-2a)
<=>4a^2-160 = 3a^2 - 6a
<=>a^2 + 6a = 160
<=>a^2 + 6a - 160= 0
<=>a^2 + 16a - 10a - 160= 0
<=>a(a +16) - 10(a +16) = 0
<=>(a +16)(a -10) = 0
+Hoặc a +16 =0 <=> a= -16(loại vì vận tốc luôn luôn dương)
+Hoặc a -10 =0 <=> a= 10 (nhận)
Vậy vận tốc dự định của người đi xe đạp là 10km/h

Gọi vận tốc dự định đi của người đó là x (km/h) (x > 0)
Thời gian dự định đi của người đó là 36/x (h)
Thời gian người đó đi nửa quãng đường đầu là 18/x (h)
Nửa quãng đường sau người đó đi với vận tốc là x + 2 (km/h) và thời gian người đó đi là 18/(x+2) (h)
Vì nghỉ lại 30 phút nên thời gian đi từ lúc xuất phát đến khi tới B là 18 x + 1 2 + 18 x + 2
Do người đó đến B chậm hơn dự kiến 12 phút = 1/5h nên ta có phương trình:
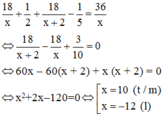
Vậy vận tốc của người đi xe đạp trên đoạn đường cuối của đoạn AB là 12 km/h
Đáp án: A

Gọi vận tốc dự định đi là x (km/h) và thời gian dự định đi là b (h)
ĐK: x,b > 0
Theo đề bài, ta có:
\(\dfrac{60}{x}-\dfrac{60}{x+5}=1\)
\(\Leftrightarrow\) \(60\left(x+5\right)-60x=x\left(x+5\right)\)
\(\Leftrightarrow x^2+5x-300=0\)
\(\Leftrightarrow\left(x-15\right)\left(x+20\right)=0\)
\(\Leftrightarrow x=15\)
=> vận tốc dự định là 15 km/h
Thời gian dự định đi là: \(\dfrac{60}{15}=4\left(h\right)\)
Em tham khảo nhé:
KO/LÀM/ĐƯỢC/BẰNG/CÁCH/LẬP/HỆ/PHƯƠNG/Ạ