Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Diện tích của mảnh vườn là: 30.20 = 600 ( m 2 )
Gọi chiều rộng của lối đi là x (0 < x < 20; m).
Sau khi làm lối đi:
Chiều rộng mảnh vườn còn lại: 20 – 2x (m)
Chiều dài mảnh vườn còn lại: 30 – 2x (m)
Vì diện tích trồng hoa bằng 84% diện tích mảnh đất nên ta có phương trình:
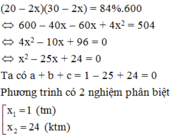
Vậy chiều rộng lối đi là 1m
Đáp án: A

Gọi chiều dài chiều rộng ban đầu là a,b
Sau khi làm lối đi thì chiều dài chiều rộng là (a -4), (b - 4)
Theo đề bài ta có
\(\hept{\begin{cases}2\left(a+b\right)=280\\\left(a-4\right)\left(b-4\right)=\:4256\end{cases}}\)
=> a = 80; b = 60

Nửa chu vi của mảnh vườn là: 280 : 2 = 140 (m )
Gọi chiều rộng mảnh vườn hình chữ nhật là x ( 0 < x \(\le\)70; m )
Chiều dài của mảnh vườn là : 140 - x (m )
Sau khi làm lối đi chiều rộng còn lại là: x - 4 (m )
Sau khi làm lối đi chiều dài còn lại là: 140 - x - 4 = 136 - x (m)
Phần diện tích để trồng trọt là: ( 136 -x ) ( x- 4 )
Theo đề bài ta có phương trình:
( 136 -x ) ( x- 4 ) = 4256
<=> x = 80 ( loại ) hoặc x = 60 ( tm)
Vậy chiều rộng là 60 m và chiều dài là 140 - 60 = 80 m.

Gọi : \(x\) là chiều dài khu vườn
Goi : \(y\) là chiều rộng khu vườn
__ vì chu vi của khu vườn hình chữ nhật là 320m , nên ta có phương trình :
\(\left(x+y\right).2=320\)
\(< =>x+y=160\) \(\left(1\right)\)
__ vi người ta làm lối đi xung quanh vườn( thuộc đất của vườn) rộng 3m va diện tích đất còn lại để trồng trọt là 5076m2 , nên ta có phương trình :
\(\left(x-3.2\right)\left(y-3.2\right)=5076\)
\(< =>\left(x-6\right)\left(y-6\right)=5076\)
\(< =>xy-6x-6y+36=5076\)
\(xy-6x-6y=5040\) \(\left(2\right)\)
Từ ( 1 ) vả ( 2 ) ta có hệ phương trình :
\(\hept{\begin{cases}x+y=160\\xy-6x-6y=5040\end{cases}}\)
BẠN GIẢI HỆ PHƯƠNG TRÌNH TRÊN RA SẼ CÓ \(x;y\). ĐÓ CHÍNH LÀ CHIỀU DÀI VÀ CHIỀU RỘNG . BẠN TỰ TÍNH NHA

Câu hỏi của Huy đức - Toán lớp 9 - Học toán với OnlineMath
