Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x(m) là chiều rộng của hcn ⇒ 4x (m) là chiều dài của hcn.
Theo đề: \((x-2).(2.4x)=x.4x+20\Leftrightarrow x^2-4x-5=0\Leftrightarrow\left[\begin{array}{} x=5\\ x=-1(loại) \end{array} \right.\)
Vậy mảnh đất hcn có chiều rộng là 5m, chiều dài là 4.5=20m

Gọi chiều dài của hình chữ nhật ban đầu là x , m , x>15 \(x\in R\)
=> Chiều rộng của hình chữ nhật ban đầu là x-15 , m
=> Diện tích của hình chữ nhật ban đầu là \(x\left(x-15\right)\) , m2
Theo bài ra ta có :
Chiều dài của hình chữ nhật mới là : x + 5 , m
Chiều rộng của hình chữ nhật mới là : x - 5 , m
=> Diện tích hình chữ nhật mới là : \(\left(x+5\right)\left(x-5\right)\) , m2
Theo giả thiết đề nên ta có phương trình :
\(\left(x+5\right)\left(x-5\right)-x\left(x-15\right)=650\)
<=> x = 35,25 m
vậy chiều dài ban đầu là 35,25 m
chiều ring ban đầu là 20,25 m

Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có: ab=280 và (a+10)(b-3)=ab+220
=>-3a+10b=250 và ab=280
=>-3a=250-10b và ab=280
=>a=10/3b-250/3 và b(10/3b-250/3)=280
=>b=28
=>a=10

Gọi chiều rộng mảnh đất ban đầu là x (m) với x>0
Gọi chiều dài mảnh đất ban đầu là y (m) với y>8
Do diện tích mảnh đất là 192 \(m^2\) nên: \(xy=192\)
Chiều dài mảnh đất sau khi giảm 8m: \(y-8\left(m\right)\)
Chiều rộng mảnh đất sau khi tăng 4m: \(x+4\left(m\right)\)
Diện tích mảnh đất lúc sau: \(\left(x+4\right)\left(y-8\right)\)
Do diện tích mảnh đất ko đổi nên: \(\left(x+4\right)\left(y-8\right)=192\)
Ta có hệ: \(\left\{{}\begin{matrix}xy=192\\\left(x+4\right)\left(y-8\right)=192\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=192\\xy-8x+4y-32=192\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=192\\2x-y+8=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\left(2x+8\right)=192\\y=2x+8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+8x-192=0\\y=2x+8\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=8\\y=24\end{matrix}\right.\)

Gọi kích thước chiều dài và chiều rộng ban đầu lần lượt là x;y (m) (x>y>3)
Diện tích mảnh đất ban đầu là: 80m2, ta có pt: xy=80 (1)
Chiều dài mảnh đất sau khi tăng 10m là: x+10 (m)
Chiều rộng mảnh đất sau khi giảm 3m là: y-3 (m)
Diện tích mới của mảnh đất là: (x+10)(y-3) (m2)
Do diện tích mới tăng thêm 20m2 nên diện tích mới khi đó là: 80+20=100 (m2)
Ta có pt:\(\left(x+10\right)\left(y-3\right)=100\) (2)
Từ (1) (2) ta có hệ: \(\left\{{}\begin{matrix}xy=80\\\left(x+10\right)\left(y-3\right)=100\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}xy=80\\xy-3x+10y-30=100\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=80\\-3x+10y=50\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}xy=80\\y=\dfrac{50+3x}{10}\end{matrix}\right.\)
\(\Rightarrow x\left(\dfrac{50+3x}{10}\right)=80\)
\(\Leftrightarrow3x^2+50x-800=0\Leftrightarrow\left(x-10\right)\left(2x+80\right)=0\)
\(\Leftrightarrow x=10\) (do 2x+80>0 với mọi x>3)
\(\Rightarrow y=8\) (tm)
Vậy kích thước chiều dài và chiều rộng ban đầu là 10m và 8m

Gọi chiều rộng của mảnh đất là x (m, x > 0).
Diện tích bằng 240 m2 ⇒ Chiều dài mảnh đất là: 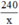 (m).
(m).
Diện tích mảnh đất sau khi tăng chiều rộng 3m, giảm chiều dài 4m là:
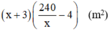
Theo bài ra: diện tích mảnh đất không đổi nên ta có phương trình:
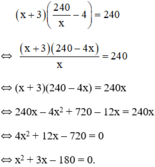
Có a = 1; b = 3; c = -180 ⇒ Δ = 32 – 4.1.(-180) = 729
Phương trình có hai nghiệm:
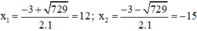
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy mảnh đất có chiều rộng bằng 12m, chiều dài bằng 240 : 12 = 20 (m).

Gọi chiều rộng là x
Chiều dài là 60-x
Theo đề, ta có: (63-x)(x+5)=x(60-x)+265
\(\Leftrightarrow63x+315-x^2-5x=60x-x^2+265\)
=>58x+315=60x+265
=>-2x=-50
=>x=25
Vậy: Chiều rộng là 25m
Chiều dài là 35m
Đặt chiều dai hình chữ nhật là a , chiều rộng là b ( \(a,b\inℝ^∗\)
Ta có hệ phương trình sau
\(\hept{\begin{cases}ab=300\\\left(a+4\right)\left(b+1\right)-ab=36\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}ab=300\\a+4b=32\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}ab=300\\a=32-4b\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}\left(32-4b\right)b=300\\a=32-4b\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}-4b^2+32b=300\\a=32-4b\end{cases}}\)