Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C

Cách giải:
Gọi ngẫu nhiên hai học sinh lên bảng trong 40 học sinh nên ta có: n Ω = C 40 2 = 780
Gọi biến cố A: “Trong hai bạn được gọi lên bảng, cả hai bạn đều tên là Anh”.
Trong lớp có 4 bạn tên là Anh nên ta có: n A = C 2 2 . C 4 2 = 6
Khi đó ta có xác suất để hai bạn được gọi lên bảng đều tên là Anh là:
P A = n A n Ω = 6 780 = 1 130

Đáp án A
Cách gọi ngẫu nhiên 2 học sinh lên bảng: C 40 2
Cách gọi 2 học sinh tên Anh lên bảng: C 4 2
⇒ p = C 4 2 C 40 2 = 1 130

Đáp án A
Cách gọi ngẫu nhiên 2 học sinh lên bảng: C 40 2
Cách gọi 2 học sinh tên Anh lên bảng: C 4 2
=> p = C 4 2 C 40 2 = 1 130

Đáp án B
Phương pháp: Xác suất : 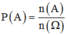
Cách giải:
Số phần tử của không gian mẫu : ![]()
Gọi A là biến cố : “4 học sinh được gọi đó cả nam lẫn nữ”
Khi đó : ![]()
Xác suất cần tìm:
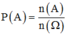
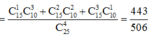

Đáp án D
Phương pháp:
TH1: An và Cường trả lời đúng, Bình trả lời sai.
TH2: Bình và Cường trả lời đúng, An trả lời sai.
Áp dụng quy tắc cộng.
Cách giải:
TH1: An và Cường trả lời đúng, Bình trả lời sai
⇒ P 1 = 0 , 9. 1 − 0 , 7 .0 , 8 = 0 , 216
TH2: Bình và Cường trả lời đúng, An trả lời sai
⇒ P 2 = 1 − 0 , 9 .0 , 7.0 , 8 = 0 , 056
Vậy xác suất cô giáo chỉ kiểm tra bài cũ đúng
3 bạn trên là P = P 1 + P 2 = 0 , 272


Coi mỗi học sinh đứng vào 1 chỗ đồng thời coi 3 học sinh tên Trang chỉ đứng vào 1 chỗ và 2 học sinh tên Huy chỉ đứng vào 1 chỗ thì còn lại 32 chỗ đứng.
Số cách sắp xếp 32 chỗ này thành 1 hàng dọc là 32!, đồng thời ta có 3! cách xếp 3 học sinh tên Trang và 2! cách xếp 2 học sinh tên Huy nên số cách sắp xếp cho 3 học sinh tên Trang đứng cạnh nhau và 2 học sinh tên Huy đứng cạnh nhau là


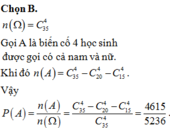

Xác suất để 2 học sinh tên Anh lên bảng là C 4 2 C 40 2 = 1 130
Chọn đáp án A.