

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
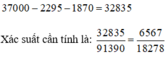
Chọn D

Chọn đáp án B.
Chọn ngẫu nhiên 5 học sinh trong 15 học sinh có C 15 5 = 3003 ⇒ n Ω = 3003
Gọi X là biến cố “tất cả các học sinh A đều được chọn”.
TH1. 2 học sinh lớp B, 0 học sinh lớp C ⇒ C 5 2 . C 7 0 = 10 cách.
TH2. 0 học sinh lớp B, 2 học sinh lớp C ⇒ C 5 0 . C 7 2 = 21 cách.
TH3. 1 học sinh lớp B, 1 học sinh lớp C ⇒ C 5 1 . C 7 1 = 35 cách.
Suy ra số phần tử của không gian mẫu là n(X)=10+21=35=66 Vậy P=2/91

Đáp án C.
Phương pháp:
Xác suất của biến cố A:
P A = n A n Ω .
Cách giải:
Số phần tử của không gian mẫu:
n Ω = C 9 3
A: “Số học sinh nam nhiều hơn số học sinh nữ”
Ta có 2 trường hợp:
+) Chọn ra 2 nam, 1 nữ:
+) Chọn ra 3 nam, 0 nữ.
⇒ n A = C 5 2 C 4 1 + C 5 3
⇒ P A = n A n Ω = C 5 2 C 4 1 + C 5 3 C 9 3 = 25 42

Chọn D.
Mỗi câu hỏi có 4 phương án trả lời nên số cách chọn phương án trả lời cho 5 câu hỏi vận dụng cao là n Ω = 4 . 4 . 4 . 4 . 4 = 4 5
Vì mỗi câu hỏi có 3 phương án trả lời sai nên số cách chọn để học sinh đó trả lời sai cả 5 câu hỏi vận dụng cao là n A = 3 . 3 . 3 . 3 . 3 = 243
Xác suất cần tìm là P A = n A n Ω = 243 4 5