Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xác suất để 2 học sinh tên Anh lên bảng là C 4 2 C 40 2 = 1 130
Chọn đáp án A.

Đáp án C

Cách giải:
Gọi ngẫu nhiên hai học sinh lên bảng trong 40 học sinh nên ta có: n Ω = C 40 2 = 780
Gọi biến cố A: “Trong hai bạn được gọi lên bảng, cả hai bạn đều tên là Anh”.
Trong lớp có 4 bạn tên là Anh nên ta có: n A = C 2 2 . C 4 2 = 6
Khi đó ta có xác suất để hai bạn được gọi lên bảng đều tên là Anh là:
P A = n A n Ω = 6 780 = 1 130

Đáp án A
Cách gọi ngẫu nhiên 2 học sinh lên bảng: C 40 2
Cách gọi 2 học sinh tên Anh lên bảng: C 4 2
⇒ p = C 4 2 C 40 2 = 1 130

Đáp án A
Cách gọi ngẫu nhiên 2 học sinh lên bảng: C 40 2
Cách gọi 2 học sinh tên Anh lên bảng: C 4 2
=> p = C 4 2 C 40 2 = 1 130

Số điểm 9 chiếm:
25%-5%=20%
Số điểm 10 và điểm 9 chiếm:
25%+20%=45%
Số học sinh lớp 5A là:
18:45x100=40(học sinh)
Đáp số:40 học sinh
Số điểm 9 chiếm trong lớp đó là :
25% - 5% = 20%
Số điểm 9 và điểm 10 chiếm trong lớp đó là :
25% + 20% = 45%
Số học sinh lớp 5A là :
18 : 45 x 100 = 40 ( học sinh )
Đáp số ; ........

Đáp án A
Bạn Nam chọn 3 trong 10 câu nên n Ω = C 10 3 = 120.
Gọi A là biến cố “Nam chọn ít nhất một câu hình học”.
Khi đó A ¯ : “Nam không chọn được câu hình học nào” hay Nam chỉ chọn toàn câu đại số
⇒ n A ¯ = C 6 3 = 20 ⇒ n A = n Ω − n A ¯ = 100 ⇒ P A = 100 120 = 5 6
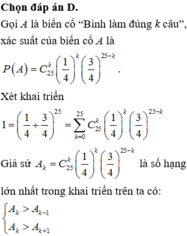
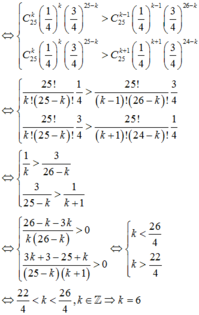

Đáp án D
Phương pháp:
TH1: An và Cường trả lời đúng, Bình trả lời sai.
TH2: Bình và Cường trả lời đúng, An trả lời sai.
Áp dụng quy tắc cộng.
Cách giải:
TH1: An và Cường trả lời đúng, Bình trả lời sai
⇒ P 1 = 0 , 9. 1 − 0 , 7 .0 , 8 = 0 , 216
TH2: Bình và Cường trả lời đúng, An trả lời sai
⇒ P 2 = 1 − 0 , 9 .0 , 7.0 , 8 = 0 , 056
Vậy xác suất cô giáo chỉ kiểm tra bài cũ đúng
3 bạn trên là P = P 1 + P 2 = 0 , 272