Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
+ Độ biến dạng của lò xo tại vị trí cân bằng
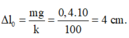
+ Đưa vật đến vị trí lò xo không biến dạng rồi thả nhẹ
+ Động năng của vật bằng thế năng lần đầu tiên tại vị trí
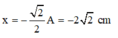
(trục Ox thẳng đứng, hướng xuống).
Lực đàn hồi có độ lớn
Chọn trục toạ độ có chiều dương hướng lên, gốc toạ độ tại vị trí cân bằng, gốc thời gian là lúc thả vật.
- Tần số góc của vật là ω = 
= 
= 20 (rad/s).
- Khi lò xo ở vị trí cân bằng: Fdh = P 
kΔ
= mg Δ = 
= 0,025m = 2,5cm.
Khi ở vị trí cân bằng lò xo dãn 2,5 cm.
- Từ vị trí cân bằng, kéo vật xuống dưới một đoạn sao cho lò xo dãn 7,5 cm tức là vật ở li độ x = 5 cm A = 
.
- Tại vị trí lò xo không bị biến dạng, vật có li độ x = 2,5 cm.
Áp dụng công thức x2 + 
v = ±ω
= ±86,6 cm/s.
Đáp án C
Phương pháp: Sử dụng lí thuyết về bài toán con lắc lò xo dao động điều hoà theo phương thẳng đứng
Cách giải:
Vật ở vị trí cân bằng thì lò xo dãn một đoạn: ∆l.
Ta có:
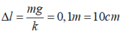
Từ vị trí cân bằng dời vật đoạn 12cm theo phương lò xo rồi buông cho dao động điều hòa => A = 12cm Vì A > ∆l nên lực đàn hồi cực tiểu tác dụng lên vật bằng 0
+ Cơ năng của con lắc là: W = 1 2 k x 2 + 1 2 m v 2 = 1 2 k 0 , 045 − Δ l 2 + 1 2 m v 2
+ Mà Δ l = m g k
® 2 W = k 0 , 045 − m g k 2 + m .0 , 4 2 = 80.10 − 3
+ Giải phương trình trên ta được: m = 0 , 25 g m = 0 , 49 g ® chọn m = 0 , 25 g
+ T = 2 π m k = 2 π 0 , 25 100 = π 10 s
Đáp án B
ü Đáp án B
+ Cơ năng của con lắc là:
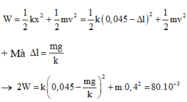
+ Giải phương trình trên ta được: m = 0 , 25 m = 0 , 49 → c h ọ n m = 0 , 25
T = 2 π m k = 2 π 0 . 25 100 = π 10 s
+ Cơ năng của con lắc là:
+ Mà ∆ l = m g k
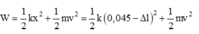
+ Giải phương trình trên ta được: m = 0 , 25 m = 0 , 49 → chọn m = 0,25 g
T = 2 π m k = 2 π 0 . 25 100 = π 10 s
ü Đáp án B
