Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Độ dài đường chéo thứ nhất là :
32 : ( 3 + 5 ) x 3 = 12 ( cm )
Độ dài đường chéo thứ hai là :
32 - 12 = 20 ( cm )
Diện tích hình thoi là :
( 20 x 12 ) : 2 = 120 ( cm2 )
Đáp số : 120 cm2

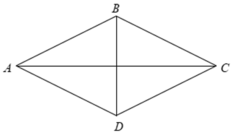
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HB = HD = 4( cm )
Theo giải thiết ta có:
PABCD = AB + BC + CD + DA = 40
⇒ AB = BC = CD = DA = 10( cm )
Áp dụng định lý Py – ta – go ta có :


Độ dài một cạnh là : 52:4=13 cm
Ta có : ED=EB nên ED=EB=BD/2=24/2=12 cm
Theo định lí Py Ta Go cho tam giác AEB vuông ta có:
AB2 = EB2 + EA2 => AE2 = AB2 - EB2 = 132 - 122 =25
=> AE = \(\sqrt{25}=5cm\)
=> AC=2AE=10cm
=> SABCD = \(\frac{1}{2}\).10.12=60 cm2


.

SBMNP=450√3cm2SBMNP=4503cm2.
Giải thích các bước giải:
Tam giác ABC có chu vi 180cm nên AB=1803=60cmAB=1803=60cm.
Do BMNP là hình thoi
⇒MN∥BP⇒MN∥BC⇒MN∥BP⇒MN∥BC.
Áp dụng định lí Ta-lét ta có:
MNBC=AMAB=BMBCMNBC=AMAB=BMBC.
Mà AM=BMAM=BM suy ra M là trung điểm của AB.
CMTT ta có N là trung điểm của AC và P là trung điểm của BC.
MP là đường trung bình của tam giác ABC.
⇒MP=12AC=12.60=30(cm)⇒MP=12AC=12.60=30(cm).
N là trung điểm của AC nên AN=12.60=30(cm)AN=12.60=30(cm).
Áp dụng định lí Pytago trong tam giác vuông ABN có:
BN=√AB2−AN2BN=√602−302BN=30√3(cm)BN=AB2−AN2BN=602−302BN=303(cm)
Vậy SBMNP=12BN.MP=12.30√3.30=450√3(cm2)

Gọi đường chéo 1 ( có tỉ lệ là 3 ) là d1
Gọi đường chéo 2 ( có tỉ lệ là 5 ) là d2
Ta có: 32 : ( 3 + 5 ) = 4
\(\Rightarrow\begin{cases}d_1=4.3\\d_2=4.5\end{cases}\)\(\Rightarrow\begin{cases}d_1=12\\d_2=20\end{cases}\)
Ta có: Shình thoi là : \(\frac{d_1.d_2}{2}=\frac{12.20}{2}=\frac{240}{2}=120\)
Vậy: Shình thoi là : \(120\)
Chúc bạn hok tốt.