K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 6 2021
`a)x=64`
`=>N=sqrtx/(sqrtx-3)=8/(8-3)=8/5`
`b)M=(2sqrtx)/(sqrtx-3)-(x+9sqrtx)/(x-9)`
`=(2x+6sqrtx-x-9sqrtx)/(x-9)`
`=(x-3sqrtx)/(x-9)`
`=sqrtx/(sqrtx+3)`
`P=M.N=x/(x-9)`
`c)` So sánh gì với 1?
26 tháng 6 2021
a) Thay x=64(TMĐK) vào N ta có:
\(N=\dfrac{\sqrt{64}}{\sqrt{64}-5}=\dfrac{8}{3}\)
Vậy x=64 thì N=\(\dfrac{8}{3}\)
b) \(P=M.N\)
\(P=\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{x-9\sqrt{x}}{x-9}.\left(\dfrac{\sqrt{x}}{\sqrt{x}-5}\right)\)
\(P=\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{x-9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\left(\dfrac{\sqrt{x}}{\sqrt{x}-5}\right)\)
\(P=\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)-x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}}{\sqrt{x}+5}\)
\(P=\dfrac{x+15\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}}{\sqrt{x}+5}\)
\(P=\dfrac{x}{\left(\sqrt{x}-3\right)\left(\sqrt{x} +3\right)}\)
\(P=\dfrac{x}{x-9}\)
N
23 tháng 11 2021
\(1,A=10\sqrt{2}+5\sqrt{2}-6\sqrt{2}=9\sqrt{2}\\ B=6\sqrt{3}-4\sqrt{3}-\sqrt{3}=\sqrt{3}\\ 2,\\ a,ĐK:1-3x\ge0\Leftrightarrow x\le\dfrac{1}{3}\\ b,ĐK:x\ge0;x\ne4\\ 3,\\ a,\Leftrightarrow12x-3=4\Leftrightarrow x=\dfrac{7}{12}\\ b,\Leftrightarrow\left|2x-1\right|=5\Leftrightarrow\left[{}\begin{matrix}2x-1=5\\1-2x=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\\ c,\Leftrightarrow\left|3x-1\right|=5\Leftrightarrow\left[{}\begin{matrix}3x-1=5\\1-3x=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\)
\(4,\\ B=\dfrac{a+2\sqrt{a}+1+a-2\sqrt{a}+1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{4\left(a+1\right)}\\ B=\dfrac{2\left(a+1\right)}{4\left(a+1\right)}=\dfrac{1}{2}\)
HQ
0
31 tháng 10 2021
Bài 2:
a: \(P=\sqrt{a}+2+\sqrt{a}+2=2\sqrt{a}+4\)
b: Để P=a+1 thì \(a-2\sqrt{a}-3=0\)
hay a=9
31 tháng 10 2021
\(2,\\ a,P=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{2-\sqrt{a}}=\sqrt{a}+2+2+\sqrt{a}=2\sqrt{a}+4\\ b,P=a+1\Leftrightarrow a-2\sqrt{a}-3=0\\ \Leftrightarrow\left(\sqrt{a}+1\right)\left(\sqrt{a}-3\right)=0\\ \Leftrightarrow\sqrt{a}=3\left(\sqrt{a}+1>0\right)\\ \Leftrightarrow a=9\left(tm\right)\\ 3,\\ a,ĐK:x\ge0;x\ne4\\ b,P=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\sqrt{x}}{\sqrt{x}+2}\\ c,P=2\Leftrightarrow2\sqrt{x}+4=2\sqrt{x}\\ \Leftrightarrow0\sqrt{x}=-4\Leftrightarrow x\in\varnothing\)
30 tháng 11 2021
d: Để (d1) vuông góc với y=(k-1)x+4 thì \(\left(k-1\right)\left(k-3\right)=-1\)
\(\Leftrightarrow k=2\)
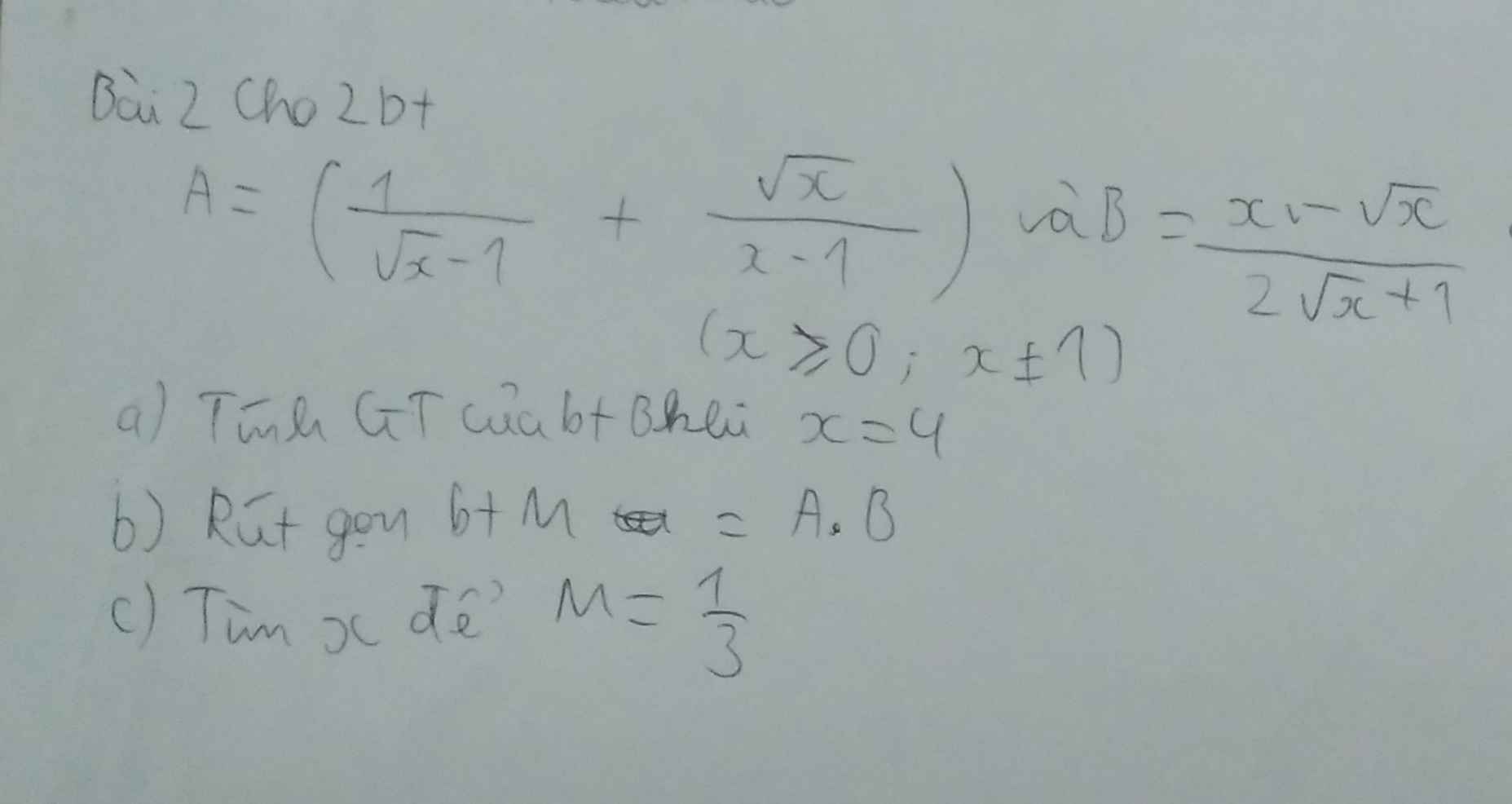
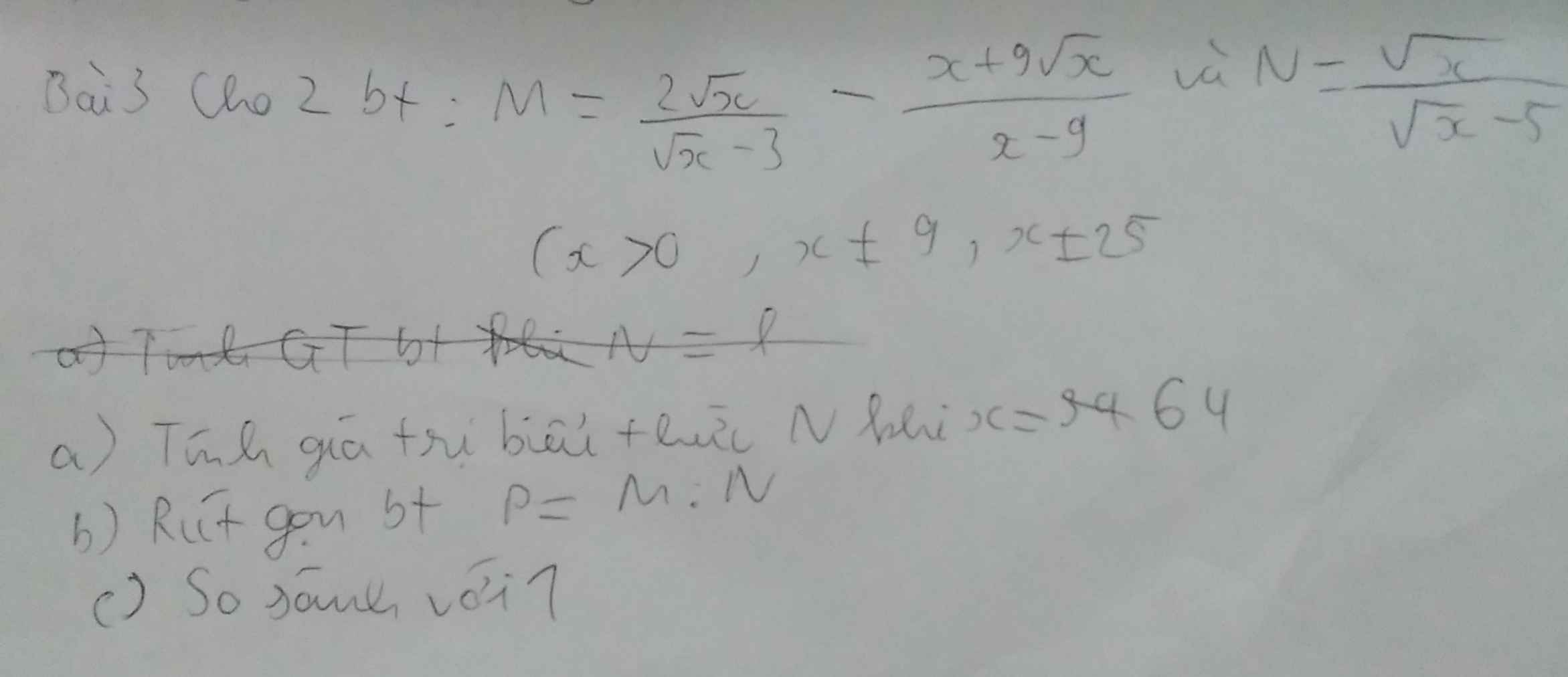
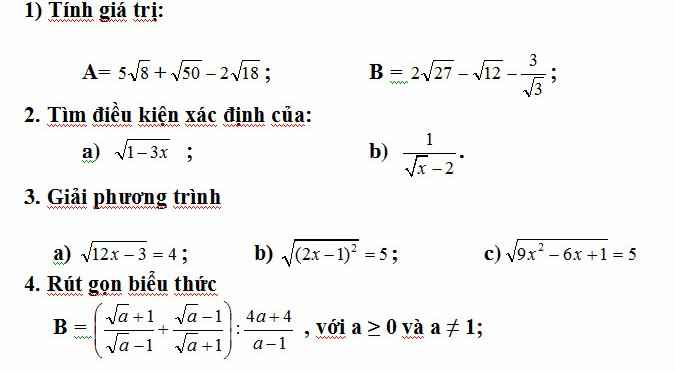
a) Thay x=4(TMĐK) vào B ta có:
\(B=\dfrac{4-\sqrt{4}}{2\sqrt{4}+1}=\dfrac{2}{5}\)
Vậy x=4 thì B=\(\dfrac{2}{5}\)
b)\(M=A.B\)
M =\(\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right).\dfrac{x-\sqrt{x}}{2\sqrt{x}+1}\)
M= \(\left(\dfrac{1}{\sqrt{x-1}}+\dfrac{\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right).\dfrac{x-\sqrt{x}}{2\sqrt{x}+1}\)
M= \(\dfrac{2\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\sqrt{x}+1}\)
M= \(\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
c)\(M=\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+1}=\dfrac{1}{3}\)
\(\Leftrightarrow3\sqrt{x}=\sqrt{x}+1\)
\(\Leftrightarrow2\sqrt{x}=1\)
\(\Leftrightarrow\sqrt{x}=\dfrac{1}{2}\)
\(\Leftrightarrow x=\dfrac{1}{4}\)
Vậy với x=\(\dfrac{1}{4}\) thì M=\(\dfrac{1}{3}\)