K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 10 2021
a: \(4-\sqrt{3-2x}=0\)
\(\Leftrightarrow3-2x=16\)
hay \(x=-\dfrac{13}{2}\)
PA
1
17 tháng 7 2021
1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
LB
1
25 tháng 8 2021
Câu 3:
2: Xét tứ giác OKEH có
\(\widehat{OKE}=\widehat{OHE}=\widehat{KOH}=90^0\)
Do đó: OKEH là hình chữ nhật
mà đường chéo OE là tia phân giác của \(\widehat{KOH}\)
nên OKEH là hình vuông
9 tháng 4 2022
\(=\dfrac{\sqrt{a}+2+\sqrt{a}-2}{a-4}:\dfrac{\sqrt{a}+2-2}{\sqrt{a}+2}\)
\(=\dfrac{2\sqrt{a}}{a-4}\cdot\dfrac{\sqrt{a}+2}{\sqrt{a}}=\dfrac{2}{\sqrt{a}-2}\)
E
1
8 tháng 8 2021
ta có sinB=\(\dfrac{AH}{AB}\)\(\Rightarrow\)AH=AB.sinB=3,6.sin62=3,18
BH=\(\sqrt{AB^2-AH^2}\)(pytago)=\(\sqrt{3,6^2-3,18^2}\)=1,69
\(_{\widehat{C}}\)=90-\(\widehat{B}\)=90-62=28\(^0\)
sinC=\(\dfrac{AB}{BC}\)\(\Rightarrow\)BC=\(\dfrac{AB}{sinC}\)=\(\dfrac{3,6}{sin28}\)=7,67
mà:CH=BC-BH=7,67-1,69=5,98
AC=\(\sqrt{BC^2-AB^2}\)(pytago)=\(\sqrt{7,67^2-3,6^2}\)=6.77
AH
Akai Haruma
Giáo viên
5 tháng 10 2021
Phần trắc nghiệm:
Hàm số bậc nhất biến $x$ có dạng $y=ax+b$ với $a, b\in\mathbb{R}, a\neq 0$.
1. A
2. C
3. A
4. B
5. B
6. A
7. B
8. C
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1
a.
Khi \(x=9\Rightarrow A=\dfrac{2\sqrt{9}}{\sqrt{9}+2}=\dfrac{6}{5}\)
b.
\(P=\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{3\sqrt{x}}{\sqrt{x}-2}-\dfrac{5x+4}{x-4}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{3\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{5x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2x-4\sqrt{x}+3x+6\sqrt{x}-5x-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2\sqrt{x}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2}{\sqrt{x}+2}\)
c.
Do \(x\ge0\Rightarrow\sqrt{x}+2\ge2\)
\(\Rightarrow\dfrac{2}{\sqrt{x}+2}\le\dfrac{2}{2}=1\)
Vậy \(P_{max}=1\) khi \(x=0\)
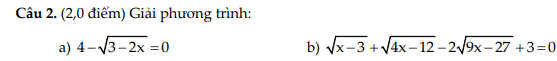
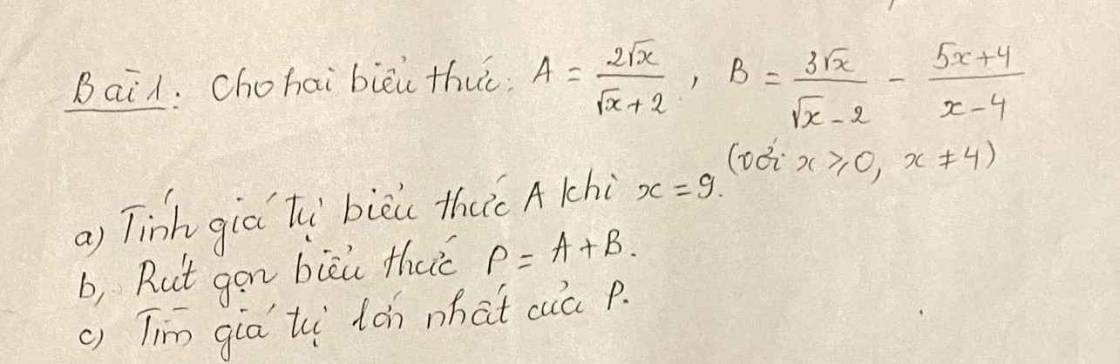
d: Để (d1) vuông góc với y=(k-1)x+4 thì \(\left(k-1\right)\left(k-3\right)=-1\)
\(\Leftrightarrow k=2\)
có 4 câu a,b,c,d mà bạn