Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐK: `x \ne kπ`
`cot(x-π/4)+cot(π/2-x)=0`
`<=>cot(x-π/4)=-cot(π/2-x)`
`<=>cot(x-π/4)=cot(x-π/2)`
`<=> x-π/4=x-π/2+kπ`
`<=>0x=-π/4+kπ` (VN)
Vậy PTVN.



\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình thoi}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(BD\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)
\(\widehat{D}=\widehat{B}=60^0\Rightarrow\Delta ACD\) đều
Đường thẳng \(AO\) cắt (SCD) tại C, mà \(OC=\dfrac{1}{2}AC\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}d\left(A;\left(SCD\right)\right)\)
Gọi M là trung điểm CD \(\Rightarrow AM\perp CD\) (do tam giác ACD đều)
\(\Rightarrow CD\perp\left(SAM\right)\)
Từ A kẻ \(AH\perp SM\Rightarrow AH\perp\left(SCD\right)\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
\(AM=\dfrac{AD\sqrt{3}}{2}=?\) (đến đây thì nhận ra bạn chép đề bài thiếu, hình thoi chưa biết độ dài cạnh)
Áp dụng hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AM^2}\Rightarrow AH=\dfrac{SA.AM}{\sqrt{SA^2+AM^2}}=?\)
\(\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}AH=?\)

2.
\(\Leftrightarrow cos2x-cos8x-sin3x+cos5x-2sin5x.cos5x=0\)
\(\Leftrightarrow2sin5x.sin3x-sin3x+cos5x-2sin5x.cos5x=0\)
\(\Leftrightarrow sin3x\left(2sin5x-1\right)-cos5x\left(2sin5x-1\right)=0\)
\(\Leftrightarrow\left(sin3x-cos5x\right)\left(2sin5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos5x=sin3x=cos\left(\dfrac{\pi}{2}-3x\right)\\sin5x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{\pi}{2}-3x+k2\pi\\5x=3x-\dfrac{\pi}{2}+k2\pi\\5x=\dfrac{\pi}{6}+k2\pi\\5x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{16}+\dfrac{k\pi}{4}\\x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{30}+\dfrac{k2\pi}{5}\\x=\dfrac{\pi}{6}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
3.
\(\Leftrightarrow1+sinx=cosx-cos3x+2sinx.cosx+1-2sin^2x\)
\(\Leftrightarrow sinx=2sin2x.sinx+2sinx.cosx-2sin^2x\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\Rightarrow x=k\pi\\1=2sin2x+2cosx-2sinx\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow4sinx.cosx+2cosx-2sinx-1=0\)
\(\Leftrightarrow2cosx\left(2sinx+1\right)-\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2cosx+1\right)\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)

Đặt \(cosx-sinx=t\Rightarrow-\sqrt{2}\le t\le\sqrt{2}\)
\(t^2=1-2sinx.cosx\Rightarrow sinx.cosx=\dfrac{1-t^2}{2}\)
Pt trở thành:
\(t\left(1+\dfrac{1-t^2}{2}\right)+1=0\)
\(\Leftrightarrow t^3-3t-2=0\)
\(\Leftrightarrow\left(t-2\right)\left(t+1\right)^2=0\Rightarrow\left[{}\begin{matrix}t=2\left(loại\right)\\t=-1\end{matrix}\right.\)
\(\Rightarrow cosx-sinx=-1\)
\(\Leftrightarrow\sqrt[]{2}cos\left(x+\dfrac{\pi}{4}\right)=-1\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=cos\left(\dfrac{3\pi}{4}\right)\)
\(\Leftrightarrow...\)

1/
PT $\Leftrightarrow \sin ^2x-(1-\sin ^2x)+\sin x-2=0$
$\Leftrightarrow 2\sin ^2x+\sin x-3=0$
$\Leftrightarrow (\sin x-1)(2\sin x+3)=0$
$\Leftrightarrow \sin x=1$ (chọn) hoặc $\sin x=-\frac{3}{2}< -1$ (loại)
Vậy $\sin x=1$
$\Leftrightarrow x=\frac{\pi}{2}+2k\pi$ với $k$ nguyên.
4/
ĐKXĐ: $\tan x\neq -1$
PT $\Rightarrow \cos ^2x(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (1-\sin ^2x)(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (1-\sin x)(1+\sin x)(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (\sin x+1)[(1-\sin x)(\cos x-1)-2(\sin x+\cos x)]=0$
$\Leftrightarrow (\sin x+1)(-1-\sin x\cos x-\sin x-\cos x)=0$
$\Leftrightarrow (\sin x+1)^2(\cos x+1)=0$
Nếu $\sin x=-1\Rightarrow x=\frac{-\pi}{2}+2k\pi$ với $k$ nguyên (tm)
Nếu $\cos x=-1\Rightarrow x=\pi +2k\pi$ với $k$ nguyên.

\(\dfrac{1}{2}sin6x\ne0\)\(\Leftrightarrow sin6x\ne0\) \(\Leftrightarrow6x\ne k\pi\)\(\Leftrightarrow x\ne\dfrac{k\pi}{6}\)
\(\dfrac{1}{2}\ne0\) rồi nên chỉ cần \(sin6x\ne0\)
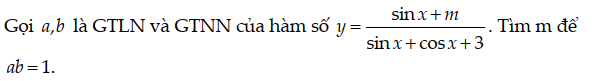
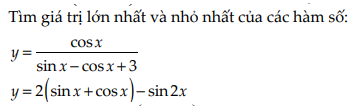
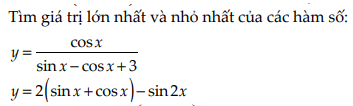

 mọi người ơi chỉ mình bài này với
mọi người ơi chỉ mình bài này với