
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



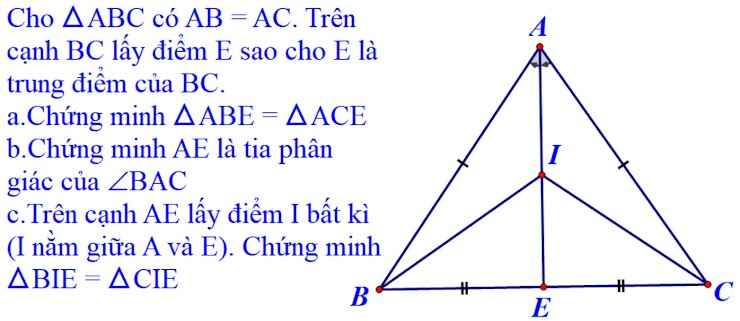
a) Xét tam giác ABE và tam giác ACE có:
+ AE chung.
+ AB = AC (gt).
+ BE = CE (E là trung điểm của BC).
=> Tam giác ABE = Tam giác ACE (c - c - c).
b) Xét tam giác ABC có: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AE là đường trung tuyến (E là trung điểm của BC).
=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).
c) Xét tam giác ABC cân tại A có:
AE là phân giác ^BAC (cmt).
=> AE là đường cao (Tính chất các đường trong tam giác cân).
=> AE \(\perp\) BC.
Xét tam giác BIE và tam giác CIE:
+ IE chung.
+ BE = CE (E là trung điểm của BC).
+ ^BEI = ^CEI ( = 90o).
=> Tam giác BIE = Tam giác CIE (c - g - c).


Vì \(x=9\Rightarrow x+1=10\)
Thay x+1=10 vào biểu thức C ta dduojcw :
\(C=x^{14}-\left(x+1\right)x^{13}+\left(x+1\right)x^{12}-...-\left(x+1\right)x+10\)
\(=x^{14}-x^{14}-x^{13}+x^{13}+x^{12}-...-x^2-x+10\)
\(=-x+10\)
\(=-9+10\)
\(=1\)

10³ + 2¹⁵
= 1000 + 32768
= 33768
Mà 33768 : 33 = 1023 (dư 9)
Em xem lại đề

bài 2
h)
\(5^x+5^x.5^3=630\)
\(5^x\left(1+5^3\right)=630\)
\(5^x.126=630\)
\(5^x=5\)
x=1
bài 2
b) \(2/3\)\(.(-5/3)+11/3.-5/3\)
\(=(2/3+11/3).(-5/3)\)
\(=-65/9\)


Bài 2:
a,gọi các góc a,b,c,d của tứ giác abcd lần lượt là a,b,c,d(a,b,c,d thuộc n,a,b,c,d<360)
=>a/1=b/2=c/3=d/4
Ta có Góc a+b+c+d=360(tổng các góc của 1 tứ giác)=>áp dung tính chất dãy tỉ số bằng nhau ta có a/1=b/2=c/3=d/4=>a+b+c+d/1+2+3+4=360/10=36
=>a=36,b=72,c=108,d=144
b,
b, Có ˆAA^+ˆDD^=36o36o+144o144o
=180o180o
mà 2 góc này ở vị trí slt
=>AB//CD
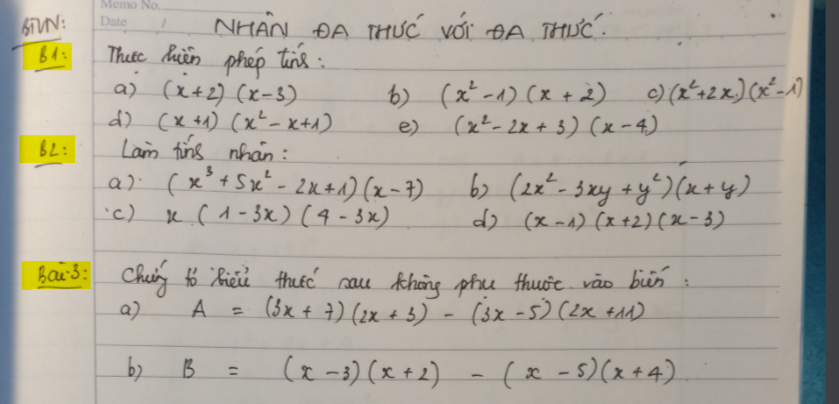


 Mọi người giúp mik câu h,i bài 2; bài 3 với
Mọi người giúp mik câu h,i bài 2; bài 3 với
Bài 2:
a) \(\left(x^3+5x^2-2x+1\right)\left(x-7\right)\\ =x^4+5x^3-2x^2+x-7x^3-35x^2+14x-7\\ =x^4-2x^3-37x^2+15x\)
b) \(\left(2x^2-3xy+y^2\right)\left(x+y\right)\\ =2x^3-3x^2y+3xy^2+2x^2y-3xy^2+y^3\\ =2x^3+y^3-x^2y\)
c) \(x\left(1-3x\right)\left(4-3x\right)=x\left(4-12x-3x+9x^2\right)=4x-15x^2+9x^3\)
d)\(\left(x-1\right)\left(x+2\right)\left(x-3\right)=\left(x^2+x-2\right)\left(x-3\right)\\ =x^3+x^2-2x-3x^2-3x+6\\ =x^3-2x^2-5x+6\)
Bài 2:
a: Ta có: \(\left(x^3+5x^2-2x+1\right)\left(x-7\right)\)
\(=x^4-7x^3+5x^3-35x^2-2x^2+14x+x-7\)
\(=x^4-2x^3-38x^2+15x-7\)
b: Ta có: \(\left(2x^2-3xy+y^2\right)\left(x+y\right)\)
\(=2x^3+2x^2y-3x^2y-3xy^2+xy^2+y^3\)
\(=2x^3-x^2y-2xy^2+y^3\)