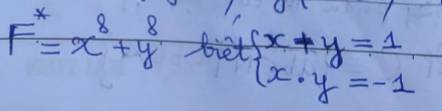Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) (Bạn tự vẽ hình ạ)
Ta có AD.AB = AE.AC
⇒ \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét \(\Delta ABC\) và \(\Delta AED\) có:
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
\(\widehat{A}:chung\)
⇒ \(\Delta ABC\sim\Delta AED\) \(\left(c.g.c\right)\)
⇒ DE // BC

a) Đặt \(a=x^2+x\)
Đa thức trở thành: \(a^2-14a+24=\left(a^2-14a+49\right)-25=\left(a-7\right)^2-25=\left(a-7-5\right)\left(a-7+5\right)=\left(a-12\right)\left(a-2\right)\)
Thay a:
\(\left(a-12\right)\left(a-2\right)=\left(x^2+x-12\right)\left(x^2+x-2\right)\)
b) Đặt \(a=x^2+x\)
Đa thức trở thành:
\(\left(x^2+x\right)^2+4x^2+4x-12=\left(x^2+x\right)^2+4\left(x^2+x\right)-12=a^2+4a-12=\left(a^2+4x+4\right)-16=\left(a+2\right)^2-16=\left(a+2-4\right)\left(a+2+4\right)=\left(a-2\right)\left(a+6\right)\)
Thay a:
\(\left(a-2\right)\left(a+6\right)=\left(x^2+x-2\right)\left(x^2+x+6\right)\)

\(5,\\ a,=x^4+4x^2+4-4x^2=\left(x^2+2\right)^2-4x^2=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\\ b,=x^4+16x^2+64-16x^2=\left(x^2+8\right)^2-16x^2=\left(x^2-4x+8\right)\left(x^2+4x+8\right)\\ c,=x^8+x^7+x^6-x^6+x^5-x^5+x^4-x^4+x^3-x^3+x^2-x^2+x-x+1\\ =x^6\left(x^2+x+1\right)-x^4\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)-x\left(x^2+x+1\right)+\left(x^2+x+1\right)\\ =\left(x^6-x^4+x^3-x+1\right)\left(x^2+x+1\right)\)
\(d,=x^8+2x^4+1-x^4=\left(x^4+1\right)^2-x^4=\left(x^4-x^2+1\right)\left(x^4+x^2+1\right)\\ =\left(x^4-x^2+1\right)\left(x^4+2x^2+1-x^2\right)\\ =\left(x^4-x^2+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)\\ e,=x^5+x^4-x^4+x^3-x^3+x^2-x^2+x+1\\ =x^3\left(x^2+x+1\right)-x^2\left(x^2+x+x\right)+\left(x^2+x+1\right)\\ =\left(x^3-x^2+1\right)\left(x^2+x+1\right)\\ f,=x^3+2x^2-x^2-2x+2x+4\\ =\left(x+2\right)\left(x^2-x+2\right)\\ g,=x^4+2x^2+1-25=\left(x^2+1\right)^2-25\\ =\left(x^2+1-5\right)\left(x^2-1-5\right)=\left(x^2-4\right)\left(x^2-6\right)=\left(x-2\right)\left(x+2\right)\left(x^2-6\right)\)
\(h,=x^3-2x^2+2x^2-4x+2x-4=\left(x-2\right)\left(x^2+2x+2\right)\\ i,=a^4-4a^2b^2+4b^4-4a^2b^2=\left(a^2-2b^2\right)^2-4a^2b^2\\ =\left(a^2-2ab-2b^2\right)\left(a^2+2ab-2b^2\right)\)

Gọi số ly trà sữa là x
=>Số ly trà đào là 210-x
Theo đề, ta có: 27000x=2*18000(210-x)
=>27000x-36000(210-x)=0
=>27000x-7560000+36000x=0
=>x=120
=>Số ly trà đào là 90 ly

\(x^2+4x+3=x^2+3x+x+3=\left(x^2+3x\right)+\left(x+3\right)=x\left(x+3\right)+\left(x+3\right)=\left(x+3\right)\left(x+1\right)\)
m.n giúp mk câu này vs ạ
(\(\dfrac{x+2}{x-2}-\dfrac{x-2}{x+2}+\dfrac{16}{4-x^2}\)) : (\(\dfrac{4}{2-x}-\dfrac{8}{2x-x^2}\))

a) Ta có: \(\left(2x-3\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\3x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\3x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{3}{2};-\dfrac{4}{3}\right\}\)
b) Ta có: \(x^3-3x^2+3x-1=\left(x-1\right)\left(x+1\right)\)
\(\Leftrightarrow\left(x-1\right)^3-\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^2-2x+1-x-1\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-3x\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=3\end{matrix}\right.\)
Vậy: S={0;1;3}
c) Ta có: \(x^2+x=2x+2\)
\(\Leftrightarrow x\left(x+1\right)-2\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
Vậy: S={-1;2}
d) Ta có: \(\left(x-1\right)^2=2\left(x^2-1\right)\)
\(\Leftrightarrow\left(x-1\right)^2-2\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-1-2x-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(-x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\-x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\-x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)Vậy: S={1;-3}
e) Ta có: \(2\left(x+2\right)^2-x^3-8=0\)
\(\Leftrightarrow2\left(x+2\right)^2-\left(x^3+8\right)=0\)
\(\Leftrightarrow2\left(x+2\right)\cdot\left(x+2\right)-\left(x+2\right)\left(x^2-2x+4\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x+4-x^2+2x-4\right)=0\)
\(\Leftrightarrow\left(x+2\right)\cdot\left(-x^2+4x\right)=0\)
\(\Leftrightarrow-x\left(x+2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=4\end{matrix}\right.\)
Vậy: S={0;-2;4}

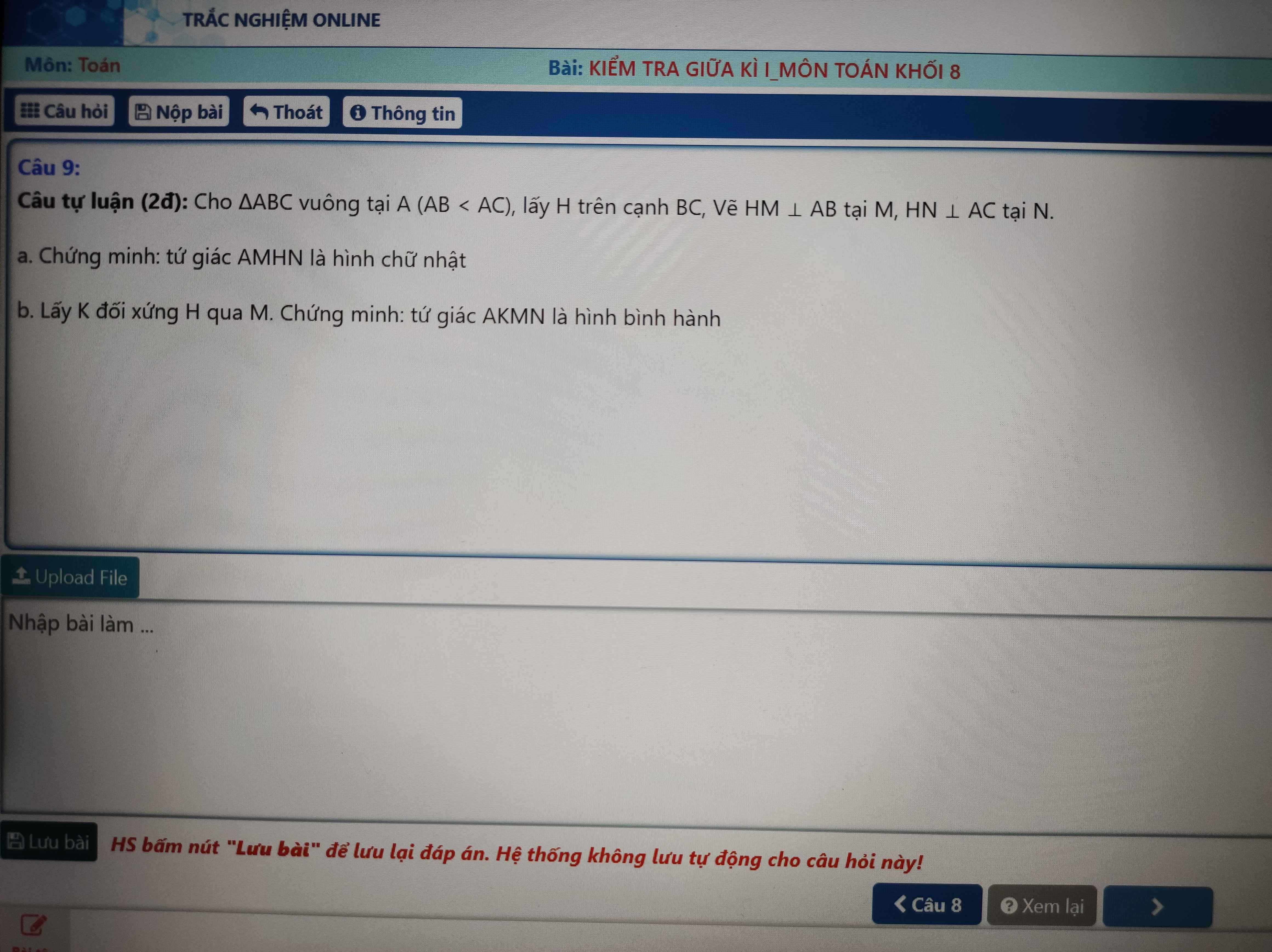
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{NAM}=90^0\)
DO đó: AMHN là hình chữ nhật

\(\left\{{}\begin{matrix}x+y=1\\xy=-1\end{matrix}\right.\)
\(F=x^8+y^8\)
\(\Leftrightarrow F=\left(x^4+y^4\right)^2-2\left(xy\right)^4\)
\(\Leftrightarrow F=\left[\left(x^2+y^2\right)^2-2\left(xy\right)^2\right]^2-2\left(xy\right)^4\)
\(\Leftrightarrow F=\left\{\left[\left(\left(x+y\right)^2-2xy\right)^2-2\left(xy\right)\right]^2\right\}^2-2\left(xy\right)^4\)
\(\Leftrightarrow F=\left\{\left[\left(\left(1\right)^2-2.\left(-1\right)\right)^2-2\left(-1\right)^2\right]\right\}^2-2\left(-1\right)^4\)
\(\Leftrightarrow F=\left\{\left[9-2\right]\right\}^2-2=49-2=47\)




 giúp tớ với ạ. Cảm ơn mọi người rất nhiều ạ
giúp tớ với ạ. Cảm ơn mọi người rất nhiều ạ