
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(=x-0,2-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(=\left(-0,2-2+2\right)+\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)\)
\(=-0,2\)
\(b,B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(=x^3-8y^3-x^3+8y^3-10\)
\(=-10\)
\(c,C=4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x-1\right)\left(x+1\right)-4x\)
\(=4\left(x^2+2x+1\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=13\)
a) \(A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(A=x-\dfrac{1}{5}-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(A=\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)-\left(\dfrac{1}{5}+2-2\right)\)
\(A=-\dfrac{1}{5}\)
Vậy: ...
b) \(B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(B=\left[x^3-\left(2y\right)^3\right]-\left[x^3-\left(2y\right)^3\right]-10\)
\(B=-10\)
Vậy: ...
c) \(4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x+1\right)\left(x-1\right)-4x\)
\(=4\left(x^2+2x+4\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=\left(4x^2+4x^2-8x^2\right)+\left(8x-4x-4x\right)+\left(4+1+8\right)\)
\(=13\)
Vậy:...

g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)

e: \(E=\dfrac{x^2-9-x^2+4-x^2+9}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x+3}\)
a: \(A=\dfrac{4x^2+x^2-2x+1+x^2+2x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{6x^2+2}{\left(x-1\right)\left(x+1\right)}\)


Lời giải:
Vì $D,E$ lần lượt là trung điểm $AB,AC$ nên $DE$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$
$\Rightarrow DE\parallel BC$ và $DE=\frac{BC}{2}=2$ (cm)
Vì $DE\parallel BC$ nên $DECB$ là hình thang
Xét hình thang $DECB$ có $M,N$ lần lượt là trung điểm của cạnh bên $BD, CE$ nên $MN$ là đường trung bình của hình thang $DECB$
$\Rightarrow MN=\frac{DE+BC}{2}=\frac{2+4}{2}=3$ (cm)



\(1,=\left(x-3\right)^2\\ 2,=\left(5+x\right)^2\\ 3,=\left(\dfrac{1}{2}x+2b\right)^2\\ 4,=\left(\dfrac{1}{3}-y^4\right)^2\\ 5,=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\\ 6,=\left(2y-5\right)\left(4y^2+10y+25\right)\\ 7,=\left(a^2-b\right)\left(a^4+a^2b+b^2\right)\\ 8,=\left(x-5\right)^2\\ 9,=8\left(x^3-\dfrac{1}{64}\right)=8\left(x-\dfrac{1}{4}\right)\left(x^2+\dfrac{1}{4}x+\dfrac{1}{16}\right)\)

\(x^3+3x^2+3x=-\dfrac{7}{8}\\ x^3+3x^2+3x+1=1-\dfrac{7}{8}\\ \left(x+1\right)^3=\dfrac{1}{8}\\ x+1=\dfrac{1}{2}\\ x=-\dfrac{1}{2}\)
Ta có: \(x^3+3x^2+3x=\dfrac{-7}{8}\)
\(\Leftrightarrow\left(x^3+3x^2+3x+1\right)=\dfrac{1}{8}\)
\(\Leftrightarrow\left(x+1\right)^3=\left(\dfrac{1}{2}\right)^3\)
\(\Leftrightarrow x+1=\dfrac{1}{2}\)
hay \(x=-\dfrac{1}{2}\)
Vậy: \(S=\left\{-\dfrac{1}{2}\right\}\)
 mng giúp ạ
mng giúp ạ 


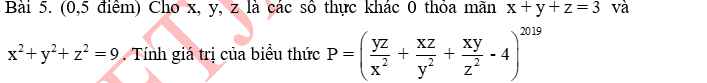
 nhờ mng giúp ạ
nhờ mng giúp ạ

 giúp e đi em xin mng đấy ạ
giúp e đi em xin mng đấy ạ