
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi số học sinh khối 6 là x
Theo đề, ta có: \(x-3\in BC\left(8;12;15\right)\)
\(\Leftrightarrow x-3\in\left\{120;240;360;...\right\}\)
\(\Leftrightarrow x\in\left\{123;243;363\right\}\)
mà 200<=x<=300
nên x=243
Gọi số học sinh khối 6 là a
a + 3 \(⋮8;12;15\)
\(\Rightarrow\) \(a+3\in BC\left(8;12;15\right)\)
8 = 2 . 3
12 = 22 . 3
15 = 3 . 5
\(\Rightarrow\) BCNN (8; 12; 15) = 22 . 3 . 5 = 60
Mà 203 < a + 3 < 303 học sinh
\(\Rightarrow\) a + 3 \(\in\) {240; 300}
\(\Rightarrow\) a \(\in\) {237; 207}

-5/7 . 2/11 + (-5/7) . 9/11 + 5/7
= -5/7 . 2/11 + -5/7 . 9/11 + (-5/7) . (-1)
= (-5/7) . (2/11 + 9/11 -1)
= (-5/7) . 0
=0
ks nha bạn

c)\(\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{3}\right)\left(1+\dfrac{1}{4}\right)....\left(1+\dfrac{1}{2020}\right)\left(1+\dfrac{1}{2021}\right)\)
\(=\left(\dfrac{1.2}{1.2}+\dfrac{1}{2}\right)\left(\dfrac{1.3}{1.3}+\dfrac{1}{3}\right)...\left(\dfrac{1.2021}{1.2021}+\dfrac{1}{2021}\right)\)
\(=\dfrac{3}{1.2}\cdot\dfrac{4}{1.3}\cdot\cdot\cdot\cdot\dfrac{2022}{1.2021}\)
\(=\dfrac{3.4.5...2022}{\left(1.1.1....1\right)\left(2.3.4...2021\right)}\)
\(=\)\(\dfrac{3.4.5...2022}{2.3.4...2021}\)
\(=\dfrac{2022}{2}=1011\)
\(d\))\(\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)....\left(1-\dfrac{1}{199}\right)\left(1-\dfrac{1}{200}\right)\)
\(=\left(\dfrac{2}{1.2}-\dfrac{1}{1.2}\right)\left(\dfrac{3}{1.3}-\dfrac{1}{1.3}\right)....\left(\dfrac{200}{1.200}-\dfrac{1}{1.200}\right)\)
\(=\dfrac{1.2.3....199}{\left(1.1.1....1\right).\left(2.3.4....200\right)}\)
\(=\dfrac{1.2.3...199}{2.3.4...200}\)
Nếu mik làm sai mong bạn thông cảm

Bài 6 :
a) 7n + 10 và 5n + 7
ƯCLN( 7n + 10 ; 5n + 7 ) = d
=> 7n + 10 chia hết d
5n + 7 chia hết d
5.(7n + 10) = 35n + 50 chia hết d
7.(5n + 7 ) = 35n + 49 chia hết d
=> ( 35n + 50 ) - ( 35n + 49 ) chia hết d
35n + 50 - 35n - 49 chia hết d
( 35n - 35n ) + ( 50 - 49 ) chia hết d
0 + 1 chia hết d
=> 1 chia hết d
suy ra d = 1
Vậy ƯCLN ( 7n + 10 ; 5n + 7 ) = 1
b) làm tương tự câu a
Bài 7 :
a) Chứng minh chia hết 4
A = 31 + 32 + 33 +... + 3119 + 3120
A = ( 31 + 32 ) + (33 + 34 ) + ... + ( 3119 + 3120 )
A = 31 . ( 1 + 3 ) + 33 . ( 1 + 3 ) + ... + 3119. ( 1 + 3 )
A = 31 . 4 + 33 . 4 + ... + 3119 . 4
A = 4. ( 31 + 33 + ... + 3119 ) chia hết 4
Chia hết cho 13 thì làm tương tự
Câu b mik chx bt làm ^.^

\(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}=\frac{1}{2.2}+\frac{1}{3.3}+\frac{1}{4.4}+...+\frac{1}{100.100}\)
\(< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{99.100}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}< 1\)(ĐPCM)

Lời giải:
$A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{19.20}$
$=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{20-19}{19.20}$
$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{19}-\frac{1}{20}$
$=1-\frac{1}{20}=\frac{19}{20}$

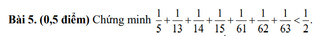

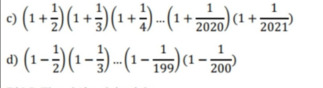


Bài 2:
\(10M=\dfrac{10^{12}+10}{10^{12}+1}=1+\dfrac{9}{10^{12}+1}\)
\(10N=\dfrac{10^{11}+10}{10^{11}+1}=1+\dfrac{9}{10^{11}+1}\)
Ta có: \(10^{12}+1>10^{11}+1\)
=>\(\dfrac{9}{10^{12}+1}< \dfrac{9}{10^{11}+1}\)
=>\(\dfrac{9}{10^{12}+1}+1< \dfrac{9}{10^{11}+1}+1\)
=>10M<10N
=>M<N
Bài 1:
\(A=\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{9}\right)\left(1-\dfrac{1}{16}\right)\cdot...\cdot\left(1-\dfrac{1}{900}\right)\)
\(=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{30}\right)\cdot\left(1+\dfrac{1}{2}\right)\cdot\left(1+\dfrac{1}{3}\right)\cdot...\cdot\left(1+\dfrac{1}{30}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{29}{30}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{31}{30}\)
\(=\dfrac{1}{30}\cdot\dfrac{31}{2}=\dfrac{31}{60}\)