
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



-5/7 . 2/11 + (-5/7) . 9/11 + 5/7
= -5/7 . 2/11 + -5/7 . 9/11 + (-5/7) . (-1)
= (-5/7) . (2/11 + 9/11 -1)
= (-5/7) . 0
=0
ks nha bạn


\(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}=\frac{1}{2.2}+\frac{1}{3.3}+\frac{1}{4.4}+...+\frac{1}{100.100}\)
\(< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{99.100}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}< 1\)(ĐPCM)

9)
Số thóc thửa ruộng thứ 1 thu hoạch được :
\(10,5\times0,2=2,1\left(tấn\right)\)
Số thóc thửa ruộng thứ 2 thu hoạch được :
\(10,5\times15\%=1,575\left(tấn\right)\)
Số thóc thửa ruộng thứ 3 thu hoạch được :
\(10,5\times\dfrac{2}{7}=3\left(tấn\right)\)
Số thóc thửa ruộng thứ 4 thu hoạch được :
\(10,5-2,1-1,575-3=3,825\left(tấn\right)\)

\(\left(\dfrac{1}{1.3}+\dfrac{1}{3.5}+...+\dfrac{1}{13.15}\right).x=\dfrac{-26}{45}\\ \Leftrightarrow\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{13.15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{13}-\dfrac{1}{15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\left(1-\dfrac{1}{15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\dfrac{14}{15}.x=\dfrac{-52}{45}\\ \Leftrightarrow x=-\dfrac{26}{21}\)
(11.3+13.5+...+113.15).x=−2645⇔(21.3+23.5+...+213.15).x=−5245⇔(1−13+13−15+...+113−115).x=−5245⇔(1−115).x=−5245⇔1415.x=−5245⇔x=−2621

\(\left(2x+3\right)^3=\left(-25\right).\left(-5\right)\)
\(\Leftrightarrow\left(2x+3\right)^3=125\)
\(\Leftrightarrow\left(2x+3\right)^3=5^3\)
\(\Leftrightarrow2x+3=5\)
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\)

\(\Leftrightarrow x\left(y+1\right)+y+1=31\\ \Leftrightarrow\left(x+1\right)\left(y+1\right)=31=31\cdot1\)
\(TH_1:\left\{{}\begin{matrix}x+1=31\\y+1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=0\end{matrix}\right.\rightarrow\left(30;0\right)\\ TH_2:\left\{{}\begin{matrix}x+1=1\\y+1=31\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=30\end{matrix}\right.\rightarrow\left(0;30\right)\)
Vậy \(\left(x;y\right)\in\left\{\left(30;0\right);\left(0;30\right)\right\}\)
\(\Leftrightarrow xy+x+y+1=31\Leftrightarrow\left(x+1\right)\left(y+1\right)=31\)
Do x, y nguyên dương nên xảy ra các TH sau:
TH1: \(\left\{{}\begin{matrix}x+1=1\\y+1=31\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=30\end{matrix}\right.\)(LOẠI)
TH2:\(\left\{{}\begin{matrix}x+1=31\\y+1=1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=0\end{matrix}\right.\)(LOẠI)
Vậy không có x, y nguyên dương thoả mãn đề bài.

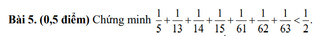
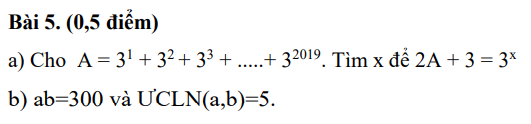

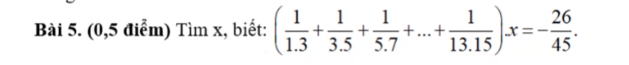
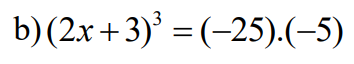
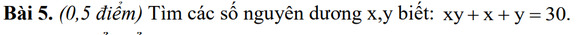
Gọi số học sinh khối 6 là x
Theo đề, ta có: \(x-3\in BC\left(8;12;15\right)\)
\(\Leftrightarrow x-3\in\left\{120;240;360;...\right\}\)
\(\Leftrightarrow x\in\left\{123;243;363\right\}\)
mà 200<=x<=300
nên x=243
Gọi số học sinh khối 6 là a
a + 3 \(⋮8;12;15\)
\(\Rightarrow\) \(a+3\in BC\left(8;12;15\right)\)
8 = 2 . 3
12 = 22 . 3
15 = 3 . 5
\(\Rightarrow\) BCNN (8; 12; 15) = 22 . 3 . 5 = 60
Mà 203 < a + 3 < 303 học sinh
\(\Rightarrow\) a + 3 \(\in\) {240; 300}
\(\Rightarrow\) a \(\in\) {237; 207}